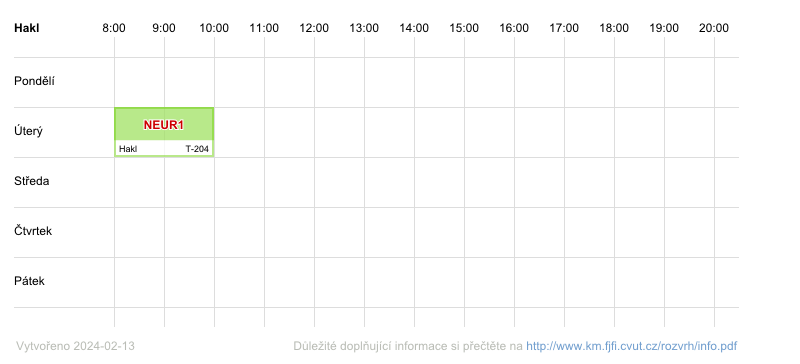
Ing. František Hakl, CSc. (externí spolupracovník)
| www: | http://www.cs.cas.cz/hakl/ |
| instituce: | ÚI AV ČR |
Databáze V3S
Aplikace V3S eviduje výsledky vědy a výzkumu a další aktivity vědecko-výzkumných pracovníků ve vědecké komunitě. Aplikace V3S slouží k odesílání výsledků do RIV, exportům pro statistické analýzy i k interním hodnocením vědecko-výzkumné činnosti.
Seznam publikaci ve V3S
za obsah této stránky zodpovídá:
Radek Fučík | naposledy změněno: 7.8.2011