prof. Dr. Ing. Michal Beneš
| e-mail: | zobrazit e-mail |
| telefon: | +420 778 546 087 |
| místnost: | 110 |
| www: | http://tjn.fjfi.cvut.cz/~benes |
Matematické modelování a numerická simulace formování mikrostruktur při fázových přechodech
| školitel: | Ing. Tomáš Oberhuber, Ph.D. |
| e-mail: | zobrazit e-mail |
| typ práce: | dizertační práce |
| zaměření: | MI_MM |
| klíčová slova: | fázové přechody, růst krystalů, růst zrn, anizotropie, matematické modelování, numerická simulace, paralelizace, MPI, Op |
| popis: | Růst krystalů při tuhnnutí materiálů, tvorba zrn a jejich vzájemná interakce i existence více fází v krystalické sktruktuře mají zásadní vliv na makroskopické fyzikální vlastnosti příslušných materiálů. Cílem práce je zabývat se 1) návrhem matematických modelů těchto jevů na úrovni kontinua, 2) formulací příslušných soustav parciálních diferenciálních rovnic v třírozměrném prostoru, a 3) návrhem a implementací efektivních numerických algoritmů pro jejich řešení na počítači. K matematickému popisu vývoje více různě orientovaných zrn lze využít metodu fázového pole (phase-field) v kombinaci s vhodnou reprezentací anizotropie povrchové energie a její orientace [3,6]. K numerickému řešení pak předpokládáme použití metody konečných objemů pro prostorovou diskretizaci na nestrukturovaných sítích, s možností adaptivního zjemnění. Časová diskretizace může být provedena implicitním Eulerovým schématem či explicitními Rungeovými-Kuttovými metodami vyššího řádu přesnosti s adaptivní volbou časového kroku. K urychlení numerických simulací bude implementován paralelní algoritmus (podobně jako např. v [1]) s využitím více CPU jader (OpenMP), více výpočetních uzlů (MPI), a případně i mnohajádrových výpočetních akcelerátorů (GPGPU s využitím technologie CUDA). |
| literatura: | [1] Strachota, P., Beneš, M. A Hybrid Parallel Numerical Algorithm for Three-Dimensional Phase Field Modeling of Crystal Growth. In ALGORITMY 2016, 20th Conference on Scientific Computing, Vysoké Tatry - Podbanské, Slovakia, March 14 - 18, 2016, Proceedings of contributed papers and posters, Comenius University, Bratislava, 2016, pp. 23-32. [2] Strachota, P., Beneš, M. Error estimate of the finite volume scheme for the Allen–Cahn equation. BIT Numer. Math. (2017). https://doi.org/10.1007/s10543-017-0687-4. [3] Strachota, P., Wodecki, A. High Resolution 3D Phase Field Simulations of Single Crystal and Polycrystalline Solidification. To appear in Acta Physica Polonica A, 2018. [4] Oberhuber, T., Numerical solution for the anisotropic Willmore flow of graphs, Applied Numerical Mathematics, Vol. 88, pp. 1-17, 2015. [5] Bauer, P., Klement, V., Oberhuber, T., Žabka, V. Implementation of the Vanka-type multigrid solver for the finite element approximation of the Navier-Stokes equations on GPU, Computer Physics Communication 200, pp. 50-56, 2016. [6] Korbuly B., Pusztai T., Henry H., Plapp M., Apel M., and Gránásy L., Grain coarsening in two-dimensional phase-field models with an orientation field, PHYSICAL REVIEW 95, pp. 053303-1 – 053303-12, 2017. [7] Gránásy L., Rátkai L., Szállás A., Korbuly B., Tóth G., Környei L., Pusztai T., Phase-Field Modeling of Polycrystalline Solidification: From Needle Crystals to Spherulites—A Review, Metall. and Mat. Trans. A, 45, pp. 1694–1719, 2014. [8] Ferreira A. F., Ferreira L. O., Assis A.C., Numerical simulation of the solidification of pure melt by a phase-field model using an adaptive computation domain, J. Braz. Soc. Mech. Sci. & Eng., 33 (2), pp. 125–130, 2011. |
| poznámka: | konzultant: Ing. Pavel Strachota, Ph.D. |
| naposledy změněno: | 14.05.2018 15:42:39 |
Dynamika křivek v rovině a prostoru a její aplikace
| školitel: | prof. Dr. Ing. Michal Beneš |
| e-mail: | zobrazit e-mail |
| typ práce: | dizertační práce |
| zaměření: | MI_MM |
| klíčová slova: | Pohyb křivek v závislosti na jejich křivosti; parametrizace; degenerované parabolické parciální rovnice; Frenetovy vzorc |
| odkaz: | http://geraldine.fjfi.cvut.cz/~benes |
| popis: | Matematické modely rozhraní nebo poruch v krystalické struktuře materiálů, vírových struktur v tekutinách nebo počítačové zpracování obrazu využívají pohybujících se křivek nebo ploch k popisu podrobností uvedených dějů. Tento popis využívá poznatků dynamiky kontinua, termodynamiky, diferenciální geometrie a teorie nelineárních evolučních parciálních diferenciálních rovnic. Obsahem tématu bude matematická a numerická analýza pohybu křivek v rovině a prostoru podle jejich křivosti, interakce několika takových křivek mezi sebou a studium jejich topologických změn. V rámci tématu by pozornost byla věnována následujícím otázkám: - formulace a matematická analýza úloh současného pohybu a interakce více křivek mezi sebou; - formulace a matematická analýza úloh anizotropního pohybu křivek; - stabilita dlouhodobých numerických výpočtů; - moderní metody implementace numerických algoritmů; - souvislosti získaných výsledků s aplikacemi; Možné aplikace výsledků práce na tématu bude možné najít v oblasti matematického modelování prostorové dynamiky a interakce svazku dislokací v materiálech a při matematické modelování pohybu vírových struktur v tekutinách. Ověření výsledků proběhne formou publikací v impaktovaných odborných časopisech a prezentacemi na mezinárodních odborných konferencích. Problematika tohoto tématu určeného pro obor Matematické inženýrsví doktorského studijního programu Aplikace přírodních věd je součástí dlouhodobé spolupráce KM FJFI ČVUT se zahraničními pracovišti, zejména s Univerzitou v Kanazawě, Univerzitou Meiji v Tokiu a Colorado School of Mines v Goldenu. Téma též navazuje na probíhající výzkum v dané oblasti podporovaný projekty GAČR, MZ ČR a OPVV. |
| literatura: | [1] M. A. Grayson: Shortening Embedded Curves. The Annals of Mathematics, Second Series, 129(1):71-111, 1989. [2] T. F. Banchoff and S. T. Lovett: Differential Geometry of Curves and Surfaces. CRC Press, ISBN 9781568814568, 2010. [3] P. Burchard, L.T. Cheng, B. Merriman and S. Osher: Motion of curves in three spatial dimensions using a level set approach. Journal of Computational Physics, 170:720-741, 2001. [4] D. J. Altschuler, S. J. Altschuler, S. B. Angenent and L. F. Wu: The Zoo of Solitons for Curve Shortening in Rn. Nonlinearity, 26(5):1189-1226, 2013. [5] M. Kolář, M. Beneš and D. Ševčovič: Area Preserving Geodesic Curvature Driven Flow of Closed Curves on a Surface. Discrete and Continuous Dynamical Systems - Series B, 22(10):3671-3689, 2017. [6] P. Pauš, M. Beneš, M. Kolář and J. Kratochvíl: Dynamics of dislocations described as evolving curves interacting with obstacles, Modelling and Simulation in Materials Science and Engineering, vol. 24, no. 3, 99. 035003, 2016. |
| naposledy změněno: | 14.05.2018 21:47:24 |
Matematické modelování strukturálních změn v materiálech
| školitel: | prof. Dr. Ing. Michal Beneš |
| e-mail: | zobrazit e-mail |
| typ práce: | dizertační práce |
| zaměření: | MI_MM |
| klíčová slova: | Cahnova - Hilliardova teorie fázových přechodů; zákony zachování; strukturální změny |
| odkaz: | http://geraldine.fjfi.cvut.cz/~benes |
| popis: | Fázové přechody v materiálech doprovázené změnou hustoty jsou popsány pomocí zákonů zachování hmoty, energie i hybnosti, poskytujících informaci o fázovém stavu, teplotě a mechanických vlastnostech ve zkoumaném objemu. Tyto modely mají podobu soustav evolučních parciálních diferenciálních rovnic. Jejich řešení vyžaduje zvládnutí více časových a prostorových měřítek. Matematická a numerická analýza proto využívaji variačních metod, teorie dynamických systémů a rovnic matematické fyziky pro získání potřebných vlastností. Obsahem tématu bude matematická a numerická analýza evolučních parciálních diferenciálních rovnic daných Cahnovou - Hilliardovou teorií fázových přechodů a statikou kontinua řešených v kontextu fázových přechodů doprovázených strukturálními změnami. V rámci tématu by pozornost byla věnována následujícím otázkám: - formulace a matematická analýza soustav nelineárních evolučních parciálních diferenciálních rovnic Cahnova-Hilliardova typu; - propojení s rovnicemi pro zachování hybnosti; - výzkum možných zobecnění pro vícesložkové a vícefázové systémy; - návrh a implementace vhodných numerických algoritmů pro jejich řešení; - moderní metody implementace numerických algoritmů na paralelních výpočetních systémech; - souvislosti získaných výsledků s modelováním fázových přechodů. Možné aplikace výsledků práce na tématu bude možné najít v oblasti matematického modelování fázových přechodů ve slitinách a formování tzv. omega-fáze v titanu a v matematické modelování procesů doprovázejících formování nanostruktur. Ověření výsledků proběhne formou publikací v impaktovaných odborných časopisech a prezentacemi na mezinárodních odborných konferencích. Problematika tohoto tématu určeného pro obor Matematické inženýrsví doktorského studijního programu Aplikace přírodních věd je součástí dlouhodobé spolupráce KM FJFI ČVUT se zahraničními pracovišti, zejména s Univerzitou v Kanazawě, Shibaura Institute of Science and Technology v Tokiu a UCLA. Téma též navazuje na probíhající výzkum v dané oblasti podporovaný projekty GAČR a OPVV. |
| literatura: | [1] H. K. Yeddu and T. Lookman, Phase-field modeling of the beta to omega phase transformation in ZrNb alloys, Materials Science and Engineering A 634 (2015) 46–54 [2] M. Mamivand, M. A. Zaeem, H. El Kadiri: A review on phase field modeling of martensitic phase transformation, Computational Materials Science 77 (2013) 304–311 [3] A. Artemev, Y. Jin and A. G. Khatchaturyan: Three-Dimensional Phase Field Model of Proper Martensitic Transformation, Acta Mater. 49 (2001) 1165–1177 [4] Strachota P. and Beneš M. Error estimate of the finite volume scheme for the Allen–Cahn equation. BIT Numer. Math. (2017). Published online: 1.670. 1-19. [5] Mach J., Beneš M. and Strachota P. Nonlinear Galerkin Finite Element Method Applied to the System of Reaction-Diffusion Equations in One Space Dimension. Comput. Math. Appl. 73 (2017), pp. 2053-2065 [5] Hoang Dieu H., Beneš M. and Oberhuber T. Numerical Simulation of Anisotropic Mean Curvature of Graphs in Relative Geometry, Acta Polytechnica Hungarica Vol. 10, No. 7, 2013 pp. 99--115 [6] Hoang, D. H., Beneš, M., and J. Stráský, Anisotropic Phase Field Model of Heteroepitaxial Growth. Acta Physica Polonica A, Vol. 128, Issue 4 (2015), pp. 520--522 [7] M. Beneš, M. Kimura, and S. Yazaki. Second order numerical scheme for motion of polygonal curves with constant area speed. Interfaces and Free Boundaries, 11(4):515–536, 2009. |
| naposledy změněno: | 14.05.2018 21:57:55 |
Diferenciální rovnice a chaos
| školitel: | prof. Dr. Ing. Michal Beneš |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM |
| klíčová slova: | evoluční diferenciální rovnice; chaotický atraktor; ljapunovské exponenty; nelineární dynamika; |
| odkaz: | http://geraldine.fjfi.cvut.cz/~benes |
| popis: | Correspondances:\\ La Nature est un temple où de vivants piliers\ Laissent parfois sortir de confuses paroles;\ L'homme y passe à travers des forêts de symboles\ Qui l'observent avec des regards familiers.\ (Charles Baudelaire, Les Fleurs du Mal, 1857) Téma je skryto v těchto verších. |
| literatura: | [1] Guckenheimer, J. and Holmes, P. (1983) Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer, New York. [2] Wiggins, S. (2003) Introduction to Applied Nonlinear Dynamical Systems and Chaos, Springer, New York. [3] Hirsch, M.W., Smale S. and Devaney R.L. (2013) Differential Equations, Dynamical Systems, and an Introduction to Chaos, Elsevier, Amsterdam. |
| naposledy změněno: | 02.04.2019 20:03:54 |
Dynamika křivek ve třírozměrném prostoru
| školitel: | prof. Dr. Ing. Michal Beneš |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MINF |
| klíčová slova: | evoluční diferenciální rovnice; diferenciální geometrie; paramerizace; střední křivost; torze; |
| odkaz: | http://geraldine.fjfi.cvut.cz |
| popis: | Téma se zabývá pohybovým zákonem křivek ve tvaru rychlost = křivost + síla v prostoru. Tento zákon pochází z fyzikálních úloh týkajících se fázových přechodů, mechaniky vlákenných struktur nebo turbulentního proudění. Uvedený zákon není zcela matematicky prozkoumán a je možné pokračovat ve výsledcích dosažených na školícím pracovišti. mezi zajímavé matematické otázky patří existence řešení, jeho spojitá závislost na parametrech nebo vztah pohybující se křivky k podmnožinám třírozměrného prostoru. |
| literatura: | [1] Kolář M., Beneš M. and Ševčovič D. Area Preserving Geodesic Curvature Driven Flow of Closed Curves on a Surface. Discrete Continuous Dynamical Systems B, Volume 22, Issue 10, December 2017, 3671--3689, doi:10.3934/dcdsb.2017148 [2] Minarčík J., Kimura M., Beneš M., Comparing Motion of Curves and Hypersurfaces in $\\mathbb{R}^m$, accepted to Discrete Continuous Dynamical Systems B, 2018 [3] Minarčík J. Dynamika pohybu křivek ve třírozměrném prostoru a její aplikace, diplomová práce, školitel M. Beneš, KM FJFI ČVUT 2018 |
| naposledy změněno: | 02.04.2019 20:02:12 |
Matematické modelování šíření elektrických signálů v myokardu
| školitel: | prof. Dr. Ing. Michal Beneš |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MINF |
| klíčová slova: | Spirálové vlny v excitovatelném prostředí; Hodgkinův-Huxleyho a Fitzův-Hughův-Nagumovův systém rovniců |
| odkaz: | http://geraldine.fjfi.cvut.cz/~benes/mb_home.html |
| popis: | Téma je zaměřeno na studium pokročilého modelu šíření elektrického signálu v excitovatelném prostředí stěn srdečních stěn. Heterogenity tototo prostředí způsobené poškozením stěn mohou způsobit vznik spirálových vln vedoucích k srdeční fibrilaci. Obsahem práce je prozkoumání matematických vlastností uvedenéh modelu a jeho součástí, jejich numerické řešení v heterogenním prostředí a posouzení získaných výsledků v medicínckém kontextu. Motivací pro téma je spolupráce v oblasti cardio-MRI a elektrkardiologie s IKEM Praha a INRIA Paris, data a zkušenosti získané touto spoluprací. |
| literatura: | Murray J.D. Mathematical Biology, Springer Verlag, 2002 Colli Franzone, Piero, Pavarino, Luca Franco & Scacchi, Simone. Mathematical Cardiac Electrophysiology. Cham: Springer, 2014 Izhikevich, Eugene M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. Cambridge, Mass.: MIT Press, 2007. Macfarlane, Peter W., et al., eds. Comprehensive Electrocardiology. 2nd ed. London: Springer, 2011. Veneroni, Marco. Reaction–diffusion systems for the macroscopic bidomain model of the cardiac electric field. Nonlinear Analysis: Real World Applications [online]. 2009, 10(2), 849–868 |
| naposledy změněno: | 02.06.2020 10:24:12 |
Matematické metody v relativistické hydrodynamice
| školitel: | prof. Dr. Ing. Michal Beneš, prof. Dr. Boris Tomášik |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM |
| klíčová slova: | zákony zachování; Minkowského a Milneho souřadnice; simulace jaderných srážek |
| odkaz: | http://geraldine.fjfi.cvut.cz/~benes/mb_home.html |
| popis: | Téma je zaměřeno na studium zákonů zachování a principů dynamiky tekutin ve stavu rovnováhy, ve stavu poblíž rovnováhy a ve stavu nerovnovážném. Relativistická hydrodynamika se uplatňuje například v popisu jaderných srážek při nejvyšších energiích. Odvození odpovídajících zákonů využívá souřadných systémů a veličin které jsou vhodné pro opis těchto srážek. Cílem tématu se seznámení s matematickými postupy v dané oblasti zahrnující formulaci klasických zákonů zachování a jejich analogie v relativistické hydrodynamice, hydrodynamické rozvoje v gradientech, Borelovu sumaci, asymtotické metody a pokročilé metody analýzy obyčejných a parciálních diferenciálních rovnic. Práce na tématu je založena na spolupráci kateder matematiky a fyziky v dané oblasti. Kontakt: michal.benes@fjfi.cvut.cz, boris.tomasik@fjfi.cvut.cz |
| literatura: | P. Romatschke and U. Romatschke, Relativistic Fluid Dynamics In and Out of Equilibrium, Cambridge University Press 2019. Jaiswal, Sunil & Chattopadhyay, Chandrodoy & Jaiswal, Amaresh & Pal, Subrata & Heinz, Ulrich. (2019). Exact solutions and attractors of higher-order viscous fluid dynamics for Bjorken flow. Physical Review C. 100. 10.1103/PhysRevC.100.034901. M. P. Heller and M. Spaliński, Hydrodynamics Beyond the Gradient Expansion: Resurgence and Resummation, Physical Review Letters 115, 072501 (2015). |
| naposledy změněno: | 04.06.2020 21:19:32 |
Stochastický model anomální difuze
| školitel: | doc. Ing. Jaromír Kukal, Ph.D., prof. Dr. Ing. Michal Beneš |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF, APIN |
| klíčová slova: | anomální difuze, markovovské řetězce, simulace Monte Carlo, porovnání modelů |
| popis: | Anomální difuze je jev, při kterém dochází k výjimkám ze zákonitostí Brownova pohybu migrujících částic. Nejčastěji pomocí ní popisujeme transport částic v turbulentním nebo porézním prostředí, kde Fickovy zákony difuze selhávají. Vlastní práce je zaměřena na jednorozměrné diskrétní modely anomální difuze, jejichž popis vede na markovovské řetězce. Ty je možné studovat jak teoreticky, tak experimentálně, a následně porovnat výsledky simulačních experimentů s očekávanými hodnotami. Důležité je rovněž porovnání volné anomální difuze a jejího omezení okrajovými podmínkami nebo porovnání s Birkhamovou aproximací studované difuze. Předpokladem je znalost matematické statistiky a programování v MATLABu. |
| literatura: | [1] Pozrikidis, C., The Fractional Laplacian, Taylor and Francis (2016)
[2] Kukal, J., Tran, Q.V., Benes, M., Discovery of Rare Event Testing for Stochastic Simulations of Diffusion Processes, Physica A: Statistical Mechanics and its Applications, 525(4) (2019) |
| naposledy změněno: | 12.03.2022 23:25:54 |
Mathematical Modelling of Moving Boundary Problems
| školitel: | prof. Dr. Ing. Michal Beneš |
| e-mail: | zobrazit e-mail |
| typ práce: | dizertační práce |
| zaměření: | MI_MM |
| klíčová slova: | nonlinear evolution problems; parametric method; levelset method; degenerate diffusion; surface diffusion; |
| odkaz: | http://geraldine.fjfi.cvut.cz/~benes/ |
| popis: | Investigation of free-boundary problems is impotrant in physical or biological context, in material science and fluid dynamics. Free boundaries are understood as hypersurfaces described by geometrical means, dynamically evolving due to the forces arising in governing partial differential equations. The entire problem becomes nonlinear and its mathematical treatment non-trivial. Closer analysis of these problems and their role in mathematical modelling lead to further improvements including incorporation of anisotropy as additional feature of the environment (crystalline lattice or surface energy density). In the Ph.D. project, a class of moving boundary problems will be investigated. Such problems are described by the law for the normal velocity of the interface incorporating mean curvature, Gaussian curvature and their differentials. The research in progress is carried out for the problems of pure advection used for fluid-component tracking, for the problems of curvature-dependent evolution up to the problems of surface diffusion. The scope of the law within the project is given by the following particular cases: mean-curvature flow relating the normal velocity of the interface to its mean curvature, constrained mean-curvature flow preserving the area enclosed by the interface, surface diffusion containing the surface Laplacian of curvature. The mathematical treatment of the motion law is based on methods directly tracking the position of or on methods yielding the position of the interface as a consequence of the solution of a higherdimensional problem. In any case, it leads to analysis of nonlinear degenerate partial differential equations, mostly of parabolic type. Applications of moving-boundary problems can be found in many areas of science. Variety of free-interface phenomena accompany processes in the material science - solidification processes, redistribution of the grain boundaries, elastic effects in materials, motion of material defects. The topic also finds rich application in computer image processing. e.g. in medical context. This project is designed for the Ph.D. degree in Mathematical Engineering and fits into the long-term international collaboration of the Department of Mathematics, e.g. with the Kanazawa University, Meiji University in Japan, Colorado School of Mines, Golden and TU Dresden. It is expected to lead to the impacted publications and to contributions in international conferences. |
| literatura: | [1] G.-Q. Chen , H. Shahgholian,J.-L. Vazquez: Free boundary problems: the forefront of current and future developments. Phil. Trans. R. Soc. A373: 20140285, 2015 [2] T. F. Banchoff and S. T. Lovett: Differential Geometry of Curves and Surfaces. CRC Press, New York, 2010. [3] S. Osher, R. Fedkiw: Level Set Methods and Dynamic Implicit Surfaces. Springer Verlag, New York, 2003. [4] M. Beneš, M. Kolář and D. Ševčovič: Curvature driven flow of a family of interacting curves with applications, Math. Meth. Appl. Sci. 43:4177–4190, 2020. [5] M. Beneš, M. Kolář and D. Ševčovič: Qualitative and Numerical Aspects of a Motion of a Family of Interacting Curves in Space, SIAM Journal on Applied Mathematics, Vol. 82, Iss. 2, 10.1137/21M1417181, 2022. |
| naposledy změněno: | 02.11.2022 11:04:28 |
Segmentace obrazu v analýze mikrostruktury zirkoniových slitin
| školitel: | Ing. Pavel Strachota, Ph.D. (FJFI ČVUT v Praze), Ing. Jakub Krejčí, Ph.D. (UJP Praha, a.s.) |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF, APIN |
| klíčová slova: | Segmentace obrazu; dynamika křivek; konvoluční neuronové sítě, zirkoniové slitiny; analýza mikrostruktury |
| odkaz: | http://saint-paul.fjfi.cvut.cz/base/cs/topics-for-students |
| popis: | 
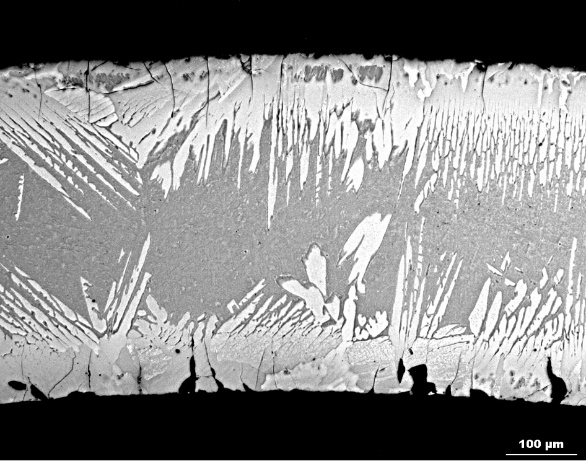
Automatická segmentace obrazu je klasická úloha počítačové grafiky, jejímž cílem je vyznačit v obraze útvary, které označují jistý objekt či strukturu. Podle charakteru obrazu někdy postačí elementární metody založené na prahování barev, jindy je třeba vzít v úvahu vliv šumu, apriorní informaci o geometrii hledaného útvaru apod. K tomu existují metody založené na dynamice křivek, řešené pomocí parciálních diferenciálních rovnic [1] i moderní metody založené na strojovém učení a konvolučních neuronových sítích [2]. Účelem práce je seznámit se s vybranými metodami po teoretické i praktické (implementační) stránce a vyzkoušet jejich efektivitu na obrazech krystalické mikrostruktury na řezu pokrytí palivové tyče jaderného reaktoru. Toto pokrytí je vyrobeno ze slitin zirkonia a při podmínkách panujících v reaktoru, nebo hypotetických havarijních situacích dochází k oxidaci materiálu [3,4]. Vznikají velmi rozličné a komplikované struktury, kdy se vrstva oxidu prolíná s vrstvou kovu. Téma je vypsáno ve spolupráci FJFI se společností UJP PRAHA a.s., která realizuje výzkum v této oblasti a může poskytnout obrazová data získaná z experimentů bez přítomnosti paliva. Zapojení do uvedené tématiky otevírá perspektivu využití vyvinutých algoritmů i uplatnění absolventa v zajímavé inženýrské praxi. |
| literatura: | [1] M. Beneš, V. Chalupecký, K. Mikula. Geometrical image segmentation by the Allen–Cahn equation, Appl. Num. Math 51 (2004), pp. 187-205, https://doi.org/10.1016/j.apnum.2004.05.001
[2] S. Minaee, Y. Boykov, F. Porikli, A. Plaza, N. Kehtarnavaz and D. Terzopoulos. Image Segmentation Using Deep Learning: A Survey, in IEEE Transactions on Pattern Analysis and Machine Intelligence 44 (7) (2022), pp. 3523-3542, https://doi.org/10.1109/TPAMI.2021.3059968. [3] C. Schneider et al., Microstructural Analysis of Zirconia at the Fuel‑Cladding Interface in Medium and High Burnup Irradiated Fuel Rods. Oxidation of Metals (2021) 96:295–306, https://doi.org/10.1007/s11085-021-10045-8 [4] T. Sawabe et al, Microstructure of oxide layers formed on zirconium alloy by air oxidation, uniform corrosion and fresh-green surface modification. J. Nuclear Mater. 419 (2011), pp. 310-319, https://doi.org/10.1016/j.jnucmat.2011.05.028 |
| naposledy změněno: | 22.08.2023 14:25:48 |
Mathematical Modeling in Cardiac Electrophysiology
| školitel: | prof. Dr. Ing. Michal Beneš |
| e-mail: | zobrazit e-mail |
| typ práce: | dizertační práce |
| zaměření: | MI_MM |
| klíčová slova: | electrophysiology; excitable media; FitzHugh–Nagumo model; Sobolev spaces; electromechanics |
| odkaz: | http://geraldine.fjfi.cvut.cz/~benes/mb_home.html |
| popis: | Abstract: Treatment of serious cardiovascular diseases requires medicine to collaborate with variety of other scientific areas including mathematics. Mathematical models can help in simulating phenomena accompanying activity of myocardium as well as they can help in designing laboratory experiments with samples of myocardium, or with in vivo experiments made with hearts of animals, devoted to verification of new treatment strategies. Mathematical modelling of the excitable medium of myocardium is based on nonlinear reaction-diffusion partial differential equations describing transfer of electric signal across the medium. They can be linked to electromechanics of myocardium. Within the topic, these processes will be considered in a planar geometry describing planar experiments of the LMS cuts, and in curved 3D geometry describing in vivo experiments, both performed by collaborating laboratories. Mathematical analysis of the underlying system of equations can be performed using the framework of weak solutions in Sobolev spaces provided crucial properties of the Galerkin approximation are shown by the method of invariant regions, apriori estimates and the compactness method. Numerical solution will be obtained by means of the finite-volume and finite-element method in space and the Runge-Kutta method in time. Computational studies will address two-dimensional and three-dimensional behavior of the solution using algorithms prepared by the student. The topic is designed for the Ph.D. degree in Mathematical Engineering. It is motivated by the collaboration with the Department of Physiology of the Faculty of Natural Sciences, and with the Institute of Physiology of the First Faculty of Medicine, Charles University in Prague. It also belongs to the framework of collaboration with the Kanazawa University, the Meiji University, and the Shibaura Institute of Technology in Japan. It is expected to lead to the impacted publications and to contributions in international conferences. |
| literatura: | [1] J. Keener and J. Sneyd, Mathematical Physiology, Springer, New York, 2009. [2] P. Colli Franzone, L.F. Pavarino and S. Scacchi, Mathematical Cardiac Electrophysiology, Springer, Heidelberg, 2014. [3] S.A. Niederer, J. Lumens and N.A. Trayanova, Computational models in cardiology. Nat Rev Cardiol 16, 100–111 (2019). [4] M. Fedele et al., A comprehensive and biophysically detailed computational model of the whole human heart electromechanics, Computer Methods in Applied Mechanics and Engineering, Volume 410, 2023, 115983. [5] J. Kantner, M. Beneš, Mathematical Model of Signal Propagation in Excitable Media, Discrete and Continuous Dynamical Systems S, 2021, 14(3) 935--951. [6] M. Beneš, M. Kolář, J. M. Sischka, A. Voigt, Degenerate area preserving surface Allen-Cahn equation and its sharp interface limit, arXiv:2303.04018, accepted to International Journal of Numerical and Applied Mathematics (2024). |
| naposledy změněno: | 09.12.2024 09:46:46 |
Databáze V3S
Aplikace V3S eviduje výsledky vědy a výzkumu a další aktivity vědecko-výzkumných pracovníků ve vědecké komunitě. Aplikace V3S slouží k odesílání výsledků do RIV, exportům pro statistické analýzy i k interním hodnocením vědecko-výzkumné činnosti.
Seznam publikaci ve V3S
Články v časopisech
2014
Pauš, P. and Kratochvíl, J. and Beneš, M., Mechanisms controlling the cyclic saturation stress and the critical cross-slip annihilation distance in copper single crystals, Philosophical Magazine Letters 94 (2014) , 45-52
BiBTeX
BiBTeX
@ARTICLE{Paus14:21082,
title = {{Mechanisms controlling the cyclic saturation stress and the critical cross-slip annihilation distance in copper single crystals}},
author = {Pau{\v s}, P. and Kratochv{\'\i}l, J. and Bene{\v s}, M.},
journal = {Philosophical Magazine Letters},
year = {2014},
volume = {94},
number = {2},
pages = {45--52},
month = {January}
}
title = {{Mechanisms controlling the cyclic saturation stress and the critical cross-slip annihilation distance in copper single crystals}},
author = {Pau{\v s}, P. and Kratochv{\'\i}l, J. and Bene{\v s}, M.},
journal = {Philosophical Magazine Letters},
year = {2014},
volume = {94},
number = {2},
pages = {45--52},
month = {January}
}
2009
Beneš, M. and Knobloch, P. and Tsujikawa, T. and Yazaki, S., Special Issue Editorial, Kybernetika 45 (2009) , 565-566
BiBTeX
BiBTeX
@ARTICLE{Benes09:1645,
title = {{Special Issue Editorial}},
author = {Bene{\v s}, M. and Knobloch, P. and Tsujikawa, T. and Yazaki, S.},
journal = {Kybernetika},
year = {2009},
volume = {45},
number = {4},
pages = {565--566}
}
title = {{Special Issue Editorial}},
author = {Bene{\v s}, M. and Knobloch, P. and Tsujikawa, T. and Yazaki, S.},
journal = {Kybernetika},
year = {2009},
volume = {45},
number = {4},
pages = {565--566}
}
Beneš, M. and Knobloch, P. and Tsujikawa, T. and Yazaki, S., Special Issue - Czech Japanese Seminar in Applied Mathematics 2008, Kybernetika 45 (2009) , 565-688
BiBTeX
BiBTeX
@ARTICLE{Benes09:1645,
title = {{Special Issue - Czech Japanese Seminar in Applied Mathematics 2008}},
author = {Bene{\v s}, M. and Knobloch, P. and Tsujikawa, T. and Yazaki, S.},
journal = {Kybernetika},
year = {2009},
volume = {45},
number = {4},
pages = {565--688}
}
title = {{Special Issue - Czech Japanese Seminar in Applied Mathematics 2008}},
author = {Bene{\v s}, M. and Knobloch, P. and Tsujikawa, T. and Yazaki, S.},
journal = {Kybernetika},
year = {2009},
volume = {45},
number = {4},
pages = {565--688}
}
2007
Beneš, M. and Kimura, M. and Nakaki, T., Editorial, Kybernetika 43 (2007) , 765-766
BiBTeX
BiBTeX
@ARTICLE{Benes07:1446,
title = {{Editorial}},
author = {Bene{\v s}, M. and Kimura, M. and Nakaki, T.},
journal = {Kybernetika},
year = {2007},
volume = {43},
number = {6},
pages = {765--766}
}
title = {{Editorial}},
author = {Bene{\v s}, M. and Kimura, M. and Nakaki, T.},
journal = {Kybernetika},
year = {2007},
volume = {43},
number = {6},
pages = {765--766}
}
Články ve sbornících
Beneš, M. and Minárik, M. and Pauš, P. and Čulík, Z., Moving Boundaries in Material Science, DMHF2007 COE Conference on the Development of Dynamic Mathematics with High Functionality, (2007) , 61-64, Kyushu University
BiBTeX
BiBTeX
@INPROCEEDINGS{Benes07:1419,
title = {{Moving Boundaries in Material Science}},
author = {Bene{\v s}, M. and Min{\' a}rik, M. and Pau{\v s}, P. and {\v C}ul{\'\i}k, Z.},
address = {Fukuoka},
booktitle = {{DMHF2007 COE Conference on the Development of Dynamic Mathematics with High Functionality}},
publisher = {Kyushu University},
year = {2007},
pages = {61--64}
}
title = {{Moving Boundaries in Material Science}},
author = {Bene{\v s}, M. and Min{\' a}rik, M. and Pau{\v s}, P. and {\v C}ul{\'\i}k, Z.},
address = {Fukuoka},
booktitle = {{DMHF2007 COE Conference on the Development of Dynamic Mathematics with High Functionality}},
publisher = {Kyushu University},
year = {2007},
pages = {61--64}
}
Mikyška, J. and Beneš, M. and Illangasekare, T.H., VODA Multiphase Flow Code for Investigation of NAPL Behavior at Heterogeneous Sand Layers, Proceeding of the 2nd International Conference on Porous Media and its Applications in Science and Engineering, (2007) , -, Universita of California
BiBTeX
BiBTeX
@INPROCEEDINGS{Mikyska07:14,
title = {{VODA Multiphase Flow Code for Investigation of NAPL Behavior at Heterogeneous Sand Layers}},
author = {Miky{\v s}ka, J. and Bene{\v s}, M. and Illangasekare, T.H.},
address = {Havai},
booktitle = {{Proceeding of the 2nd International Conference on Porous Media and its Applications in Science and Engineering}},
publisher = {Universita of California},
year = {2007},
pages = {--}
}
title = {{VODA Multiphase Flow Code for Investigation of NAPL Behavior at Heterogeneous Sand Layers}},
author = {Miky{\v s}ka, J. and Bene{\v s}, M. and Illangasekare, T.H.},
address = {Havai},
booktitle = {{Proceeding of the 2nd International Conference on Porous Media and its Applications in Science and Engineering}},
publisher = {Universita of California},
year = {2007},
pages = {--}
}
Beneš, M. and Fučík, R. and Mikyška, J. and Illangasekare, T.H., Analytical and Numerical Solution for One-Dimensional Two-Phase Flow in Homogeneous Porous Medium, Proceeding of the 2nd International Conference on Porous Media and its Applications in Science and Engineering, (2007) , -, Universita of California
BiBTeX
BiBTeX
@INPROCEEDINGS{Benes07:1404,
title = {{Analytical and Numerical Solution for One-Dimensional Two-Phase Flow in Homogeneous Porous Medium}},
author = {Bene{\v s}, M. and Fu{\v c}{\'\i}k, R. and Miky{\v s}ka, J. and Illangasekare, T.H.},
address = {Havai},
booktitle = {{Proceeding of the 2nd International Conference on Porous Media and its Applications in Science and Engineering}},
publisher = {Universita of California},
year = {2007},
pages = {--}
}
title = {{Analytical and Numerical Solution for One-Dimensional Two-Phase Flow in Homogeneous Porous Medium}},
author = {Bene{\v s}, M. and Fu{\v c}{\'\i}k, R. and Miky{\v s}ka, J. and Illangasekare, T.H.},
address = {Havai},
booktitle = {{Proceeding of the 2nd International Conference on Porous Media and its Applications in Science and Engineering}},
publisher = {Universita of California},
year = {2007},
pages = {--}
}
2006
Roubal, J. and Havlena, V. and Beneš, M., Base Vectors for Solving Partial Differential Equations, Proceedings of International Control Conference, (2006) , -, University of Strathclyde
BiBTeX
BiBTeX
@INPROCEEDINGS{Roubal06:120,
title = {{Base Vectors for Solving Partial Differential Equations}},
author = {Roubal, J. and Havlena, V. and Bene{\v s}, M.},
address = {Glasgow},
booktitle = {{Proceedings of International Control Conference}},
publisher = {University of Strathclyde},
year = {2006},
pages = {--}
}
title = {{Base Vectors for Solving Partial Differential Equations}},
author = {Roubal, J. and Havlena, V. and Bene{\v s}, M.},
address = {Glasgow},
booktitle = {{Proceedings of International Control Conference}},
publisher = {University of Strathclyde},
year = {2006},
pages = {--}
}
2005
Beneš, M., Quantitative Aspects of Microstructure Formation in Solidification, EQUADIFF 11, International Conference on Differential Equations, (2005) , 5, Comenius University
BiBTeX
BiBTeX
@INPROCEEDINGS{Benes05:1418,
title = {{Quantitative Aspects of Microstructure Formation in Solidification}},
author = {Bene{\v s}, M.},
address = {Bratislava},
booktitle = {{EQUADIFF 11, International Conference on Differential Equations}},
publisher = {Comenius University},
year = {2005},
pages = {5}
}
title = {{Quantitative Aspects of Microstructure Formation in Solidification}},
author = {Bene{\v s}, M.},
address = {Bratislava},
booktitle = {{EQUADIFF 11, International Conference on Differential Equations}},
publisher = {Comenius University},
year = {2005},
pages = {5}
}
1999
Beneš, M., Simulační model tuhnutí krystalických materiálů, TRANSFER 99, (1999) , 7-8, VUT v Brně
BiBTeX
BiBTeX
@INPROCEEDINGS{Benes99:2397,
title = {{Simula{\v c}n{\'\i} model tuhnut{\'\i} krystalick{\' y}ch materi{\' a}l{\r u}}},
author = {Bene{\v s}, M.},
address = {Brno},
booktitle = {{TRANSFER 99}},
publisher = {VUT v Brn{\v e}},
year = {1999},
pages = {7--8}
}
title = {{Simula{\v c}n{\'\i} model tuhnut{\'\i} krystalick{\' y}ch materi{\' a}l{\r u}}},
author = {Bene{\v s}, M.},
address = {Brno},
booktitle = {{TRANSFER 99}},
publisher = {VUT v Brn{\v e}},
year = {1999},
pages = {7--8}
}
Ostatní publikace
2014
Beneš, M. and Strachota, P. and Mach, J., A Quasi-1D Two-Phase Model for Exhaust Pipe Flow with Condensation, 2014
BiBTeX
BiBTeX
@TECHREPORT{Benes14:2150,
title = {{A Quasi-1D Two-Phase Model for Exhaust Pipe Flow with Condensation}},
author = {Bene{\v s}, M. and Strachota, P. and Mach, J.},
address = {Praha},
institution = {Bosch, s s.r.o.},
publisher = {{\v C}VUT, Fakulta jadern{\' a} a fyzik{\' a}ln{\v e} in{\v z}en{\' y}rsk{\' a}},
year = {2014},
number = {14-01},
pages = {21}
}
title = {{A Quasi-1D Two-Phase Model for Exhaust Pipe Flow with Condensation}},
author = {Bene{\v s}, M. and Strachota, P. and Mach, J.},
address = {Praha},
institution = {Bosch, s s.r.o.},
publisher = {{\v C}VUT, Fakulta jadern{\' a} a fyzik{\' a}ln{\v e} in{\v z}en{\' y}rsk{\' a}},
year = {2014},
number = {14-01},
pages = {21}
}
2009
Beneš, M. and Tsujikawa, T. and Yazaki, S. (ed.), Proceedings of Czech-Japanese Seminar in Applied Mathematics 2008, (2009) , 79, Kyushu University
BiBTeX
BiBTeX
@PROCEEDINGS{Benes09:1537,
title = {{Proceedings of Czech-Japanese Seminar in Applied Mathematics 2008}},
address = {Fukuoka},
editor = {Bene{\v s}, M. and Tsujikawa, T. and Yazaki, S.},
publisher = {Kyushu University},
year = {2009},
pages = {79}
}
title = {{Proceedings of Czech-Japanese Seminar in Applied Mathematics 2008}},
address = {Fukuoka},
editor = {Bene{\v s}, M. and Tsujikawa, T. and Yazaki, S.},
publisher = {Kyushu University},
year = {2009},
pages = {79}
}
2008
Beneš, M., Segmentation of MRI Data Using the Partial Differential Eequation of Allen-Cahn Type, 2008
BiBTeX
BiBTeX
@UNPUBLISHED{Benes08:1526,
title = {{Segmentation of MRI Data Using the Partial Differential Eequation of Allen-Cahn Type}},
author = {Bene{\v s}, M.},
year = {2008},
note = {Unpublished Lecture}
}
title = {{Segmentation of MRI Data Using the Partial Differential Eequation of Allen-Cahn Type}},
author = {Bene{\v s}, M.},
year = {2008},
note = {Unpublished Lecture}
}
Beneš, M., Quantitative Aspects of Microstructure Formation in Solidification, 2008
BiBTeX
BiBTeX
@UNPUBLISHED{Benes08:1526,
title = {{Quantitative Aspects of Microstructure Formation in Solidification}},
author = {Bene{\v s}, M.},
year = {2008},
note = {Unpublished Lecture}
}
title = {{Quantitative Aspects of Microstructure Formation in Solidification}},
author = {Bene{\v s}, M.},
year = {2008},
note = {Unpublished Lecture}
}
Beneš, M., Recent advances in mathematical modelling and numerical simulation technology and environment - Applications in Material Science, 2008
BiBTeX
BiBTeX
@UNPUBLISHED{Benes08:1526,
title = {{Recent advances in mathematical modelling and numerical simulation technology and environment - Applications in Material Science}},
author = {Bene{\v s}, M.},
year = {2008},
note = {Unpublished Lecture}
}
title = {{Recent advances in mathematical modelling and numerical simulation technology and environment - Applications in Material Science}},
author = {Bene{\v s}, M.},
year = {2008},
note = {Unpublished Lecture}
}
2007
Beneš, M. and Kimura, M. and Nakaki, T. (ed.), Proceedings of Czech Japanese Seminar in Applied Mathematics 2006, (2007) , Kyushu University
BiBTeX
BiBTeX
@PROCEEDINGS{Benes07:1381,
title = {{Proceedings of Czech Japanese Seminar in Applied Mathematics 2006}},
address = {Fukuoka},
editor = {Bene{\v s}, M. and Kimura, M. and Nakaki, T.},
publisher = {Kyushu University},
year = {2007}
}
title = {{Proceedings of Czech Japanese Seminar in Applied Mathematics 2006}},
address = {Fukuoka},
editor = {Bene{\v s}, M. and Kimura, M. and Nakaki, T.},
publisher = {Kyushu University},
year = {2007}
}
2006
Beneš, M. and Mikyška, J. and Oberhuber, T. and Bednařík, P., Quench Tank Internal Geometry Optimization, 2006
BiBTeX
BiBTeX
@TECHREPORT{Benes06:1303,
title = {{Quench Tank Internal Geometry Optimization}},
author = {Bene{\v s}, M. and Miky{\v s}ka, J. and Oberhuber, T. and Bedna{\v r}{\'\i}k, P.},
address = {Prague},
institution = {Caterpillar, Inc.},
publisher = {Faculty of Nuclear Sciences and Physical Engineering},
year = {2006},
number = {Inter},
pages = {35}
}
title = {{Quench Tank Internal Geometry Optimization}},
author = {Bene{\v s}, M. and Miky{\v s}ka, J. and Oberhuber, T. and Bedna{\v r}{\'\i}k, P.},
address = {Prague},
institution = {Caterpillar, Inc.},
publisher = {Faculty of Nuclear Sciences and Physical Engineering},
year = {2006},
number = {Inter},
pages = {35}
}
Beneš, M. and Mikyška, J. and Oberhuber, T. and Bednařík, P., Quench Tank Internal Geometry Optimization II, 2006
BiBTeX
BiBTeX
@TECHREPORT{Benes06:1418,
title = {{Quench Tank Internal Geometry Optimization II}},
author = {Bene{\v s}, M. and Miky{\v s}ka, J. and Oberhuber, T. and Bedna{\v r}{\'\i}k, P.},
address = {Prague},
institution = {Caterpillar, Inc.},
publisher = {Faculty of Nuclear Sciences and Physical Engineering},
year = {2006},
number = {Inter},
pages = {106}
}
title = {{Quench Tank Internal Geometry Optimization II}},
author = {Bene{\v s}, M. and Miky{\v s}ka, J. and Oberhuber, T. and Bedna{\v r}{\'\i}k, P.},
address = {Prague},
institution = {Caterpillar, Inc.},
publisher = {Faculty of Nuclear Sciences and Physical Engineering},
year = {2006},
number = {Inter},
pages = {106}
}
Beneš, M. and Kimura, M. and Nakaki, T. (ed.), Proceedings of Czech-Japanese Seminar in Applied Mathematics 2005, (2006) , 157, Faculty of Mathematics, Kyushu University
BiBTeX
BiBTeX
@PROCEEDINGS{Benes06:1258,
title = {{Proceedings of Czech-Japanese Seminar in Applied Mathematics 2005}},
address = {Fukuoka},
editor = {Bene{\v s}, M. and Kimura, M. and Nakaki, T.},
publisher = {Faculty of Mathematics, Kyushu University},
year = {2006},
pages = {157}
}
title = {{Proceedings of Czech-Japanese Seminar in Applied Mathematics 2005}},
address = {Fukuoka},
editor = {Bene{\v s}, M. and Kimura, M. and Nakaki, T.},
publisher = {Faculty of Mathematics, Kyushu University},
year = {2006},
pages = {157}
}
Beneš, M. and Mikyška, J. and Oberhuber, T., Quench Tank Internal Geometry Optimization - Addendum, 2006
BiBTeX
BiBTeX
@TECHREPORT{Benes06:1418,
title = {{Quench Tank Internal Geometry Optimization - Addendum}},
author = {Bene{\v s}, M. and Miky{\v s}ka, J. and Oberhuber, T.},
address = {Prague},
institution = {Caterpillar, Inc.},
publisher = {Faculty of Nuclear Sciences and Physical Engineering},
year = {2006},
number = {Inter},
pages = {25}
}
title = {{Quench Tank Internal Geometry Optimization - Addendum}},
author = {Bene{\v s}, M. and Miky{\v s}ka, J. and Oberhuber, T.},
address = {Prague},
institution = {Caterpillar, Inc.},
publisher = {Faculty of Nuclear Sciences and Physical Engineering},
year = {2006},
number = {Inter},
pages = {25}
}
2005
Beneš, M. and Mikyška, J. and Oberhuber, T. (ed.), Proceedings of Czech - Japanese Seminar in Applied Mathematics 2004, (2005) , 206, ČVUT, Fakulta jaderná a fyzikálně inženýrská
BiBTeX
BiBTeX
@PROCEEDINGS{Benes05:1081,
title = {{Proceedings of Czech - Japanese Seminar in Applied Mathematics 2004}},
address = {Praha},
editor = {Bene{\v s}, M. and Miky{\v s}ka, J. and Oberhuber, T.},
publisher = {{\v C}VUT, Fakulta jadern{\' a} a fyzik{\' a}ln{\v e} in{\v z}en{\' y}rsk{\' a}},
year = {2005},
pages = {206}
}
title = {{Proceedings of Czech - Japanese Seminar in Applied Mathematics 2004}},
address = {Praha},
editor = {Bene{\v s}, M. and Miky{\v s}ka, J. and Oberhuber, T.},
publisher = {{\v C}VUT, Fakulta jadern{\' a} a fyzik{\' a}ln{\v e} in{\v z}en{\' y}rsk{\' a}},
year = {2005},
pages = {206}
}
1999
Beneš, M., Time Discretisation in Solution of Systems of Semi-linear Parabolic PDEs Arising in Free-boundary Problems, 1999
BiBTeX
BiBTeX
@UNPUBLISHED{Benes99:2398,
title = {{Time Discretisation in Solution of Systems of Semi-linear Parabolic PDEs Arising in Free-boundary Problems}},
author = {Bene{\v s}, M.},
year = {1999},
note = {Unpublished Lecture}
}
title = {{Time Discretisation in Solution of Systems of Semi-linear Parabolic PDEs Arising in Free-boundary Problems}},
author = {Bene{\v s}, M.},
year = {1999},
note = {Unpublished Lecture}
}
Šembera, J. and Beneš, M., Nonlinear Galerkin Method for Reaction-Diffusion Systems Admitting Invariant Regions, 1999
BiBTeX
BiBTeX
@TECHREPORT{Sembera99:25,
title = {{Nonlinear Galerkin Method for Reaction-Diffusion Systems Admitting Invariant Regions}},
author = {{\v S}embera, J. and Bene{\v s}, M.},
address = {Praha},
institution = {{\v C}VUT FJFI},
publisher = {{\v C}VUT, Fakulta jadern{\' a} a fyzik{\' a}ln{\v e} in{\v z}en{\' y}rsk{\' a}},
year = {1999},
number = {1},
pages = {17}
}
title = {{Nonlinear Galerkin Method for Reaction-Diffusion Systems Admitting Invariant Regions}},
author = {{\v S}embera, J. and Bene{\v s}, M.},
address = {Praha},
institution = {{\v C}VUT FJFI},
publisher = {{\v C}VUT, Fakulta jadern{\' a} a fyzik{\' a}ln{\v e} in{\v z}en{\' y}rsk{\' a}},
year = {1999},
number = {1},
pages = {17}
}
Beneš, M., Numerická simulace dynamiky křivek v rovině, 1999
BiBTeX
BiBTeX
@UNPUBLISHED{Benes99:2398,
title = {{Numerick{\' a} simulace dynamiky k{\v r}ivek v rovin{\v e}}},
author = {Bene{\v s}, M.},
year = {1999},
note = {Unpublished Lecture}
}
title = {{Numerick{\' a} simulace dynamiky k{\v r}ivek v rovin{\v e}}},
author = {Bene{\v s}, M.},
year = {1999},
note = {Unpublished Lecture}
}
Beneš, M., Dynamika anisotropních křivek v rovině II, 1999
BiBTeX
BiBTeX
@UNPUBLISHED{Benes99:2398,
title = {{Dynamika anisotropn{\'\i}ch k{\v r}ivek v rovin{\v e} II}},
author = {Bene{\v s}, M.},
year = {1999},
note = {Unpublished Lecture}
}
title = {{Dynamika anisotropn{\'\i}ch k{\v r}ivek v rovin{\v e} II}},
author = {Bene{\v s}, M.},
year = {1999},
note = {Unpublished Lecture}
}
Beneš, M., Mathematical Analysis of Phase-field Equations with Numerically Efficient Coupling Terms, 1999
BiBTeX
BiBTeX
@TECHREPORT{Benes99:2397,
title = {{Mathematical Analysis of Phase-field Equations with Numerically Efficient Coupling Terms}},
author = {Bene{\v s}, M.},
address = {Praha},
publisher = {{\v C}VUT, Fakulta jadern{\' a} a fyzik{\' a}ln{\v e} in{\v z}en{\' y}rsk{\' a}},
year = {1999},
number = {MMG 3},
pages = {20}
}
title = {{Mathematical Analysis of Phase-field Equations with Numerically Efficient Coupling Terms}},
author = {Bene{\v s}, M.},
address = {Praha},
publisher = {{\v C}VUT, Fakulta jadern{\' a} a fyzik{\' a}ln{\v e} in{\v z}en{\' y}rsk{\' a}},
year = {1999},
number = {MMG 3},
pages = {20}
}
Beneš, M., Dynamics of Curves in the Plane, 1999
BiBTeX
BiBTeX
@UNPUBLISHED{Benes99:2398,
title = {{Dynamics of Curves in the Plane}},
author = {Bene{\v s}, M.},
year = {1999},
note = {Unpublished Lecture}
}
title = {{Dynamics of Curves in the Plane}},
author = {Bene{\v s}, M.},
year = {1999},
note = {Unpublished Lecture}
}
Beneš, M., Diffuse Interface Approach to the Solidification of Pure Materials, 1999
BiBTeX
BiBTeX
@UNPUBLISHED{Benes99:2354,
title = {{Diffuse Interface Approach to the Solidification of Pure Materials}},
author = {Bene{\v s}, M.},
year = {1999},
note = {Unpublished Lecture}
}
title = {{Diffuse Interface Approach to the Solidification of Pure Materials}},
author = {Bene{\v s}, M.},
year = {1999},
note = {Unpublished Lecture}
}
1997
Beneš, M., Phase Field Model of Microstructure Growth in Solidification of Pure Substances, Faculty of Nuclear Sciences and Physical Engineering, 1997
BiBTeX
BiBTeX
@PHDTHESIS{Benes97:1559,
title = {{Phase Field Model of Microstructure Growth in Solidification of Pure Substances}},
author = {Bene{\v s}, M.},
address = {Prague},
year = {1997},
pages = {95},
school = {Faculty of Nuclear Sciences and Physical Engineering}
}
title = {{Phase Field Model of Microstructure Growth in Solidification of Pure Substances}},
author = {Bene{\v s}, M.},
address = {Prague},
year = {1997},
pages = {95},
school = {Faculty of Nuclear Sciences and Physical Engineering}
}
za obsah této stránky zodpovídá:
Radek Fučík | naposledy změněno: 7.8.2011