Ing. Pavel Strachota, Ph.D.
| e-mail: | zobrazit e-mail |
| telefon: | +420 778 546 112 |
| místnost: | 033a |
| www: | http://saint-paul.fjfi.cvut.cz/base/ |
Matematické modelování a numerická simulace formování mikrostruktur při fázových přechodech
| školitel: | Ing. Tomáš Oberhuber, Ph.D. |
| e-mail: | zobrazit e-mail |
| typ práce: | dizertační práce |
| zaměření: | MI_MM |
| klíčová slova: | fázové přechody, růst krystalů, růst zrn, anizotropie, matematické modelování, numerická simulace, paralelizace, MPI, Op |
| popis: | Růst krystalů při tuhnnutí materiálů, tvorba zrn a jejich vzájemná interakce i existence více fází v krystalické sktruktuře mají zásadní vliv na makroskopické fyzikální vlastnosti příslušných materiálů. Cílem práce je zabývat se 1) návrhem matematických modelů těchto jevů na úrovni kontinua, 2) formulací příslušných soustav parciálních diferenciálních rovnic v třírozměrném prostoru, a 3) návrhem a implementací efektivních numerických algoritmů pro jejich řešení na počítači. K matematickému popisu vývoje více různě orientovaných zrn lze využít metodu fázového pole (phase-field) v kombinaci s vhodnou reprezentací anizotropie povrchové energie a její orientace [3,6]. K numerickému řešení pak předpokládáme použití metody konečných objemů pro prostorovou diskretizaci na nestrukturovaných sítích, s možností adaptivního zjemnění. Časová diskretizace může být provedena implicitním Eulerovým schématem či explicitními Rungeovými-Kuttovými metodami vyššího řádu přesnosti s adaptivní volbou časového kroku. K urychlení numerických simulací bude implementován paralelní algoritmus (podobně jako např. v [1]) s využitím více CPU jader (OpenMP), více výpočetních uzlů (MPI), a případně i mnohajádrových výpočetních akcelerátorů (GPGPU s využitím technologie CUDA). |
| literatura: | [1] Strachota, P., Beneš, M. A Hybrid Parallel Numerical Algorithm for Three-Dimensional Phase Field Modeling of Crystal Growth. In ALGORITMY 2016, 20th Conference on Scientific Computing, Vysoké Tatry - Podbanské, Slovakia, March 14 - 18, 2016, Proceedings of contributed papers and posters, Comenius University, Bratislava, 2016, pp. 23-32. [2] Strachota, P., Beneš, M. Error estimate of the finite volume scheme for the Allen–Cahn equation. BIT Numer. Math. (2017). https://doi.org/10.1007/s10543-017-0687-4. [3] Strachota, P., Wodecki, A. High Resolution 3D Phase Field Simulations of Single Crystal and Polycrystalline Solidification. To appear in Acta Physica Polonica A, 2018. [4] Oberhuber, T., Numerical solution for the anisotropic Willmore flow of graphs, Applied Numerical Mathematics, Vol. 88, pp. 1-17, 2015. [5] Bauer, P., Klement, V., Oberhuber, T., Žabka, V. Implementation of the Vanka-type multigrid solver for the finite element approximation of the Navier-Stokes equations on GPU, Computer Physics Communication 200, pp. 50-56, 2016. [6] Korbuly B., Pusztai T., Henry H., Plapp M., Apel M., and Gránásy L., Grain coarsening in two-dimensional phase-field models with an orientation field, PHYSICAL REVIEW 95, pp. 053303-1 – 053303-12, 2017. [7] Gránásy L., Rátkai L., Szállás A., Korbuly B., Tóth G., Környei L., Pusztai T., Phase-Field Modeling of Polycrystalline Solidification: From Needle Crystals to Spherulites—A Review, Metall. and Mat. Trans. A, 45, pp. 1694–1719, 2014. [8] Ferreira A. F., Ferreira L. O., Assis A.C., Numerical simulation of the solidification of pure melt by a phase-field model using an adaptive computation domain, J. Braz. Soc. Mech. Sci. & Eng., 33 (2), pp. 125–130, 2011. |
| poznámka: | konzultant: Ing. Pavel Strachota, Ph.D. |
| naposledy změněno: | 14.05.2018 15:42:39 |
Řízení a optimalizace procesů popsaných parciálními diferenciálními rovnicemi
| školitel: | Ing. Aleš Wodecki, Ph.D., Ing. Pavel Strachota, Ph.D. |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF |
| klíčová slova: | teorie řízení, duální úloha, optimalizace, funkcionální analýza, numerické metody |
| popis: | Parciální diferenciální rovnice se užívají hojně k modelování přírodních jevů. Ať jde o rovnici vedení tepla nebo Schrödingerovu rovnici, zajímá nás, jak bychom mohli ovlivnit vývoj těchto procesů, aby probíhaly řízeně. Na tuto netriviální otázku lze často odpovědět s pomocí teorie řízení formulované na funkčních prostorech. Během své bakalářské/diplomové práce proniknete do vybraných partií teorie řízení. Teorii se naučíte aplikovat na problémy minimalizace funkcionálu s nekonečně dimenzionální vazbou. Tuto vazbu bude často představovat úloha pro diferenciální rovnici nebo systém diferenciálních rovnic. Vše formulujeme obecně pomocí funkcionálního počtu na Banachových nebo Hilbertových prostorech. Poté diskretizujeme problém minimalizace buď přímo, nebo užijeme duální úlohy odvozené na úrovni funkcionálního počtu, abychom navrhli efektivnější optimalizační řešič. Nakonec implementujeme navrženou metodu a ukážeme, že teoretická výstavba dává v praxi funkční způsob řízení fyzikálních procesů. Téma je vhodné pro studenty matematiky A, které zajímá praktický dopad pokročilejších partií matematiky (funkcionální analýzy) na řešení fyzikálních problémů. |
| literatura: | [1] M. Hinze, R. Pinnau, M. Ulbrich, and S. Ulbrich. Optimization with PDE
Constraints. Springer, 2009.
[2] Luise Blank, Harald Garcke, Lavinia Sarbu, Tarin Srisupattarawanit, Vanessa Styles, and Axel Voigt. Phase-field approaches to structural topol- ogy optimization. In Constrained Optimization and Optimal Control for Partial Differential Equations, International Series of Numerical Mathematics vol. 160, pp. 245--256, Springer, 2012. [3] J. Gao, B. Song, and Z. Mao. Combination of the phase field method and beso method for topology optimization. Struct. Multidisc. Optim. 61 (2020), pp. 225-237. |
| naposledy změněno: | 22.08.2023 14:30:15 |
Metody strojového učení v medicínských aplikacích
| školitel: | Ing. Tomáš Kouřim, Ing. Pavel Strachota, Ph.D. |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF, APIN |
| klíčová slova: | strojové učení, predikce, medicína, transplantace ledvin, dávkování léků, srdeční arytmie |
| popis: | Dynamicky se rozvíjející startup Mild Blue, který založili absolventi FJFI Ing. Tomáš Kouřim a Ing. Jan Kubant, nabízí spolupráci studentům ve formě vedení bakalářských i diplomových prací. Společnost se zabývá aplikací metod strojového učení v různých oblastech medicíny. Je možné se zabývat např. následujícími tématy:
1. Predikce přežití štěpu po transplantaci ledvin pomocí strojového učení na základě reálných dat o transplantacích ledvin provedených od roku 2005 v IKEM. 2. Optimalizace dávkováni léků pomocí metod umělé inteligence. Na základě dat z již vyvinuté aplikace sloužící k výpočtu dávkování je možné teoreticky hodnotit různé alternativy a vytvořit model, který by se mohl stát základem budoucí klinické studie. 3. Speech2text v medicíně. Jedná se o zapojení do již probíhajícího vývoje softwarového nástroje k rozpoznávání řeči. Součástí práce by bylo i získávání, resp. úprava datové sady pro trénování příslušného algoritmu. 4. Použiti strojového vidění pro redigitalizaci lékařských zpráv. K dispozici je rozsáhlá databáze lékařských zpráv, kterou však lze zpracovávat na úrovni studentské práce až po anonymizaci. 5. Predikce srdečních arytmií pomocí neuronových sítí na základě historické datové sady čítající desetitisíce vzorků anotovaných lékaři (spolupráce s IKEM). |
| poznámka: | Kontakt:
Ing. Tomáš Kouřim https://mild.blue/ tomas.kourim@mild.blue tel. + 420 723 927 536 Ing. Jan Kubant jan.kubant@mild.blue Ing. Pavel Strachota, Ph.D. pavel.strachota@fjfi.cvut.cz |
| naposledy změněno: | 24.09.2021 13:23:19 |
Stochastický model anomální difuze
| školitel: | doc. Ing. Jaromír Kukal, Ph.D., prof. Dr. Ing. Michal Beneš |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF, APIN |
| klíčová slova: | anomální difuze, markovovské řetězce, simulace Monte Carlo, porovnání modelů |
| popis: | Anomální difuze je jev, při kterém dochází k výjimkám ze zákonitostí Brownova pohybu migrujících částic. Nejčastěji pomocí ní popisujeme transport částic v turbulentním nebo porézním prostředí, kde Fickovy zákony difuze selhávají. Vlastní práce je zaměřena na jednorozměrné diskrétní modely anomální difuze, jejichž popis vede na markovovské řetězce. Ty je možné studovat jak teoreticky, tak experimentálně, a následně porovnat výsledky simulačních experimentů s očekávanými hodnotami. Důležité je rovněž porovnání volné anomální difuze a jejího omezení okrajovými podmínkami nebo porovnání s Birkhamovou aproximací studované difuze. Předpokladem je znalost matematické statistiky a programování v MATLABu. |
| literatura: | [1] Pozrikidis, C., The Fractional Laplacian, Taylor and Francis (2016)
[2] Kukal, J., Tran, Q.V., Benes, M., Discovery of Rare Event Testing for Stochastic Simulations of Diffusion Processes, Physica A: Statistical Mechanics and its Applications, 525(4) (2019) |
| naposledy změněno: | 12.03.2022 23:25:54 |
Využití strojového učení pro řešení fázového problému v krystalografii
| školitel: | Dr.rer.nat. Lukáš Palatinus, Ing. Pavel Strachota, Ph.D., |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF |
| klíčová slova: | elektronová difrakce, fázový problém, krystalografie, neuronové sítě, strojové učení |
| odkaz: | http://www.fzu.cz/vyzkum/vyzkumne-sekce-a-oddeleni/sekce-3/oddeleni-19/laborator-1901 |
| popis: | Elektronová krystalografie se zabývá určováním atomární struktury pomocí elektronového záření, zejména elektronové difrakce. V laboratoři elektronové difrakce Fyzikálního ústavu AV ČR jsme schopni s pomocí transmisního elektronového mikroskopu a dalších přístrojů odhalit prostorovou organizaci atomů v krystalech, avšak získaná syrová data je nejprve nutné zpracovat náročnými počítačovými algoritmy.
Měření poskytují údaje o intenzitách (amplitudách) různých frekvencí zastoupených v elektronové hustotě, avšak nikoliv o jejich fázových posunutích. Aby bylo možné získat prostorové rozložení této hustoty v krystalu pomocí inverzní Fourierovy transformace, je nutné vyřešit takzvaný fázový problém. Pro řešení tohoto problému bylo vyvinuto a úspěšně použito několik algoritmů, avšak každý z nich má svá omezení. Tématem práce je ověření možností metod strojového učení, zejména neuronových sítí, v této oblasti. Úspěšná aplikace strojového učení na řešení fázového problému by mohla přinést významný pokrok v oboru krystalografie. Téma je vhodné pro studenty, kteří se nebojí programování a implementace algoritmů v oblasti dnes velmi populárních metod strojového učení, ale zároveň jsou ochotni si rozšířit znalosti z matematiky a fyziky. Výhodou je přímá spolupráce s experimentálním pracovištěm a přístup k takřka neomezenému množství reálných dat použitelných pro trénování modelů.  |
| literatura: | [1] C. C. Aggarwal - Neural Networks and Deep Learning, Springer, 2018.
[2] T. Hastie, R. Tibshirani, J. Friedman – The Elements of Statistical Learning, Data Mining, Inference, and Prediction. 2nd. ed., Springer-Verlag New York, 2009. [3] C. Giacovazzo (ed.): Fundamentals of Crystallography, 3. vydání, Oxford University Press (2011), https://academic.oup.com/book/371 [4] L. Palatinus: The charge flipping algorithm in crystallography. Acta Crystallographica A69, 1-16 (2013), https://doi.org/10.1107/S2052519212051366 |
| naposledy změněno: | 22.08.2023 14:26:09 |
Segmentace obrazu v analýze mikrostruktury zirkoniových slitin
| školitel: | Ing. Pavel Strachota, Ph.D. (FJFI ČVUT v Praze), Ing. Jakub Krejčí, Ph.D. (UJP Praha, a.s.) |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF, APIN |
| klíčová slova: | Segmentace obrazu; dynamika křivek; konvoluční neuronové sítě, zirkoniové slitiny; analýza mikrostruktury |
| odkaz: | http://saint-paul.fjfi.cvut.cz/base/cs/topics-for-students |
| popis: | 
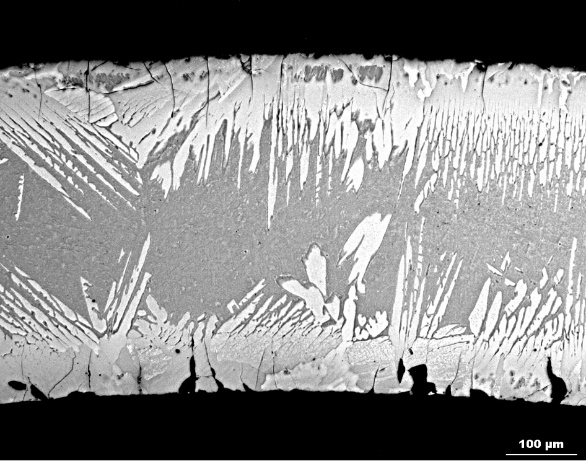
Automatická segmentace obrazu je klasická úloha počítačové grafiky, jejímž cílem je vyznačit v obraze útvary, které označují jistý objekt či strukturu. Podle charakteru obrazu někdy postačí elementární metody založené na prahování barev, jindy je třeba vzít v úvahu vliv šumu, apriorní informaci o geometrii hledaného útvaru apod. K tomu existují metody založené na dynamice křivek, řešené pomocí parciálních diferenciálních rovnic [1] i moderní metody založené na strojovém učení a konvolučních neuronových sítích [2]. Účelem práce je seznámit se s vybranými metodami po teoretické i praktické (implementační) stránce a vyzkoušet jejich efektivitu na obrazech krystalické mikrostruktury na řezu pokrytí palivové tyče jaderného reaktoru. Toto pokrytí je vyrobeno ze slitin zirkonia a při podmínkách panujících v reaktoru, nebo hypotetických havarijních situacích dochází k oxidaci materiálu [3,4]. Vznikají velmi rozličné a komplikované struktury, kdy se vrstva oxidu prolíná s vrstvou kovu. Téma je vypsáno ve spolupráci FJFI se společností UJP PRAHA a.s., která realizuje výzkum v této oblasti a může poskytnout obrazová data získaná z experimentů bez přítomnosti paliva. Zapojení do uvedené tématiky otevírá perspektivu využití vyvinutých algoritmů i uplatnění absolventa v zajímavé inženýrské praxi. |
| literatura: | [1] M. Beneš, V. Chalupecký, K. Mikula. Geometrical image segmentation by the Allen–Cahn equation, Appl. Num. Math 51 (2004), pp. 187-205, https://doi.org/10.1016/j.apnum.2004.05.001
[2] S. Minaee, Y. Boykov, F. Porikli, A. Plaza, N. Kehtarnavaz and D. Terzopoulos. Image Segmentation Using Deep Learning: A Survey, in IEEE Transactions on Pattern Analysis and Machine Intelligence 44 (7) (2022), pp. 3523-3542, https://doi.org/10.1109/TPAMI.2021.3059968. [3] C. Schneider et al., Microstructural Analysis of Zirconia at the Fuel‑Cladding Interface in Medium and High Burnup Irradiated Fuel Rods. Oxidation of Metals (2021) 96:295–306, https://doi.org/10.1007/s11085-021-10045-8 [4] T. Sawabe et al, Microstructure of oxide layers formed on zirconium alloy by air oxidation, uniform corrosion and fresh-green surface modification. J. Nuclear Mater. 419 (2011), pp. 310-319, https://doi.org/10.1016/j.jnucmat.2011.05.028 |
| naposledy změněno: | 22.08.2023 14:25:48 |
Fázové přechody v zirkonia a difuzní procesy
| školitel: | prof. Dr. Ing. Michal Beneš (FJFI ČVUT v Praze), Ing. Jakub Krejčí, Ph.D. (UJP Praha, a.s.) |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF |
| klíčová slova: | zirkoniové slitiny; metoda fázového pole; fázový diagram; anizotropie; teorie fázových přechodů; metoda konečných objemů |
| popis: | 
 Téma se věnuje matematickému modelování fázových přechodů v krystalické struktuře materiálů na bázi zirkonia, ze kterého je vyrobena struktura palivových tyčí jaderných reaktorů. Tyto fázové přechody pod vlivem rostoucí teploty výrazně mění mechanické vlastnosti materiálu. Jejich znalost přispívá k prodloužení životnosti a zvýšení spolehlivosti. Cílem tématu je seznámení se s principy modelování těchto fázových přechodů s využitím zákonů zachování hmoty a energie a termodynamiky, vlastnosti a numerické řešení výsledných parciálních diferenciálních rovnic a využití dosud známých výsledků v této oblasti. Perspektivou vedoucí k diplomové práci je návrh dvou a třírozměrného matematického modelu a jeho numerické řešení moderními metodami. Téma je motivováno reálnými požadavky provozu jaderných elektráren a je realizováno ve spolupráci s UJP PRAHA a.s., Zbraslav. Zapojení do uvedené tématiky otevírá perspektivu uplatnění absolventa v praxi.
Téma se věnuje matematickému modelování fázových přechodů v krystalické struktuře materiálů na bázi zirkonia, ze kterého je vyrobena struktura palivových tyčí jaderných reaktorů. Tyto fázové přechody pod vlivem rostoucí teploty výrazně mění mechanické vlastnosti materiálu. Jejich znalost přispívá k prodloužení životnosti a zvýšení spolehlivosti. Cílem tématu je seznámení se s principy modelování těchto fázových přechodů s využitím zákonů zachování hmoty a energie a termodynamiky, vlastnosti a numerické řešení výsledných parciálních diferenciálních rovnic a využití dosud známých výsledků v této oblasti. Perspektivou vedoucí k diplomové práci je návrh dvou a třírozměrného matematického modelu a jeho numerické řešení moderními metodami. Téma je motivováno reálnými požadavky provozu jaderných elektráren a je realizováno ve spolupráci s UJP PRAHA a.s., Zbraslav. Zapojení do uvedené tématiky otevírá perspektivu uplatnění absolventa v praxi. |
| literatura: | [1] Jaworska L, Cyboron J, Cygan S, Zwolinski A, Onderka B, Skrzekut T. Zirconium Phase Transformation under Static High Pressure and ω-Zr Phase Stability at High Temperatures. Materials (Basel). 2019 Jul 12;12(14):2244. https://doi.org/10.3390/ma12142244.
[2] Lin, C., Ruan, H. & Shi, SQ. Mechanical–chemical coupling phase-field modeling for inhomogeneous oxidation of zirconium induced by stress–oxidation interaction. npj Mater Degrad 4, 22 (2020). https://doi.org/10.1038/s41529-020-00125-6 [3] Bo-Yuan Ning, Pressure-induced structural phase transitions of zirconium: an ab initio study based on statistical ensemble theory, 2022, J. Phys.: Condens. Matter 34 505402 https://doi.org/10.1088/1361-648X/ac9bbf |
| naposledy změněno: | 22.08.2023 18:18:08 |
Matematické modelování strukturální dynamiky palivových tyčí
| školitel: | prof. Dr. Ing. Michal Beneš (FJFI ČVUT v Praze), Ing. Jakub Krejčí, Ph.D. (UJP Praha, a.s.) |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF |
| klíčová slova: | metoda konečných prvků; plastická deformace; fázové přechody v krystalické struktuře; palivové tyče jaderného reaktoru; |
| popis: | 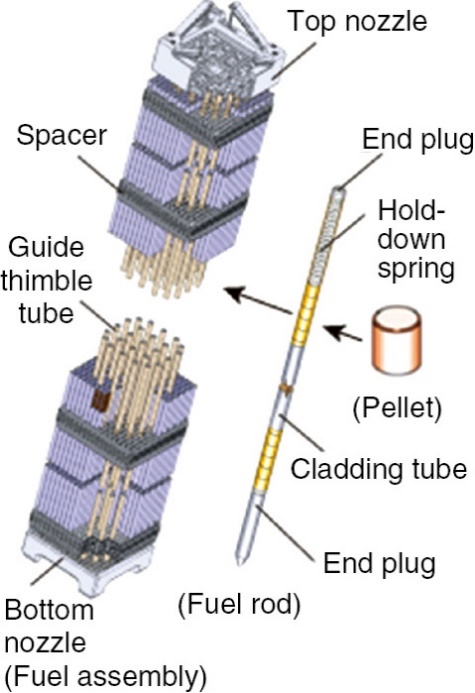
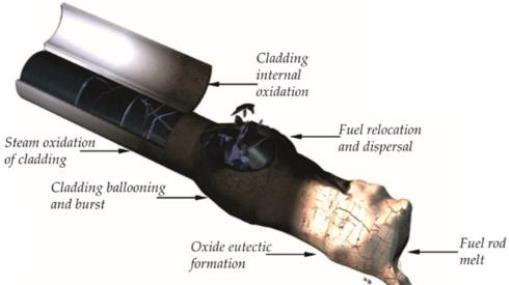 Námětem je matematický model deformací ve struktuře palivové tyče jaderného reaktoru při působení vysokého napětí a vysokých teplot typických pro hypotetické havarijní situace. Při těchto podmínkách dochází ke změnám ve vlastnostech krystalické struktury a měknutí materiálu, ze kterého je palivová tyč vyrobena. Cílem tématu je seznámení se základními principy modelování elastické a plastické deformace pomocí parciálních diferenciálních rovnic a jejich numerického řešení na výkonné výpočetní technice. Perspektivou vedoucí k diplomové práci je návrh plně třírozměrného matematického modelu a jeho porovnání s již existujícími přístupy. Téma je motivováno reálnými požadavky provozu jaderných elektráren a je realizováno ve spolupráci s UJP PRAHA a.s., Zbraslav. Zapojení do uvedené tématiky otevírá perspektivu uplatnění absolventa v praxi.
Námětem je matematický model deformací ve struktuře palivové tyče jaderného reaktoru při působení vysokého napětí a vysokých teplot typických pro hypotetické havarijní situace. Při těchto podmínkách dochází ke změnám ve vlastnostech krystalické struktury a měknutí materiálu, ze kterého je palivová tyč vyrobena. Cílem tématu je seznámení se základními principy modelování elastické a plastické deformace pomocí parciálních diferenciálních rovnic a jejich numerického řešení na výkonné výpočetní technice. Perspektivou vedoucí k diplomové práci je návrh plně třírozměrného matematického modelu a jeho porovnání s již existujícími přístupy. Téma je motivováno reálnými požadavky provozu jaderných elektráren a je realizováno ve spolupráci s UJP PRAHA a.s., Zbraslav. Zapojení do uvedené tématiky otevírá perspektivu uplatnění absolventa v praxi. |
| literatura: | [1] Jinsu K., Jeong Whan Y., Hyochan K., Sung-Uk L., Prediction of ballooning and burst for nuclear fuel cladding with anisotropic creep modeling during Loss of Coolant Accident (LOCA), Nuclear Engineering and Technology, 53:10, 2021, 3379--3397, https://doi.org/10.1016/j.net.2021.04.020.
[2] Manngard T., Massih A.R. Modelling and Simulation of Reactor Fuel Cladding under Loss-of-Coolant Accident Conditions, Journal of Nuclear Science and Technology, 48:1, 2011, 39--49, https://doi.org/10.1080/18811248.2011.9711677 [3] Guenot-Delahaie I., Sercombe J., Federici E., Bernaudat C., Largenton R., et al. Investigation of clad ballooning during NSRR RIA tests using ALCYONE fuel performance code. Journal of Nuclear Materials, 2022, 562, pp.153584. https://doi.org/10.1016/j.jnucmat.2022.153584. cea-03713987 |
| naposledy změněno: | 22.08.2023 18:18:16 |
Molekulové simulace nukleace při adiabatické expanzi
| školitel: | prof. RNDr. Jiří Kolafa, CSc., Ing. David Celný, Ph.D. |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF, APIN |
| klíčová slova: | molekulová dynamika, nukleace, GPU, HPC |
| odkaz: | http://ufch.vscht.cz/research/researchgroups/statistical_thermodynamics |
| popis: | Téma klimatu stále více rezonuje v celospolečenské diskusi. Jedním z jevů, jehož modelování je důležité pro pochopení procesů v atmosféře, je nukleace[1], tedy tvorba kapiček a ledových krystalků. Porozumění tomuto fenoménu je nezbytné pro přesnější modelování srážkových vzorců, distribuci vlhkosti a aerosolových částic v atmosféře. Proces nukleace má uplatnění i v mnoha dalších oblastech (produkce nanočástic, termomechanika aj.)
Tato práce se zaměřuje na využití molekulových simulací k zachycení chování kontrolovaně ochazované páry. Proces ochlazování může být řízen přímo jevem, který je zároveň simulován na spojité úrovni (supersonická expanze do vakua a rovnice fluidní dynamiky), nebo může být dán vnějším protokolem (mlžná komora). Obě tyto situace mají svou relevanci a je možné je simulovat pomocí nově vyvinutého paralelního programu[2,3], který bude moci zájemce použít, případně rozšířit pro případ složitějších systémů obsahující organické látky a/nebo nosný plyn. Součástí práce je seznámení s fyzikálními základy řešené problematiky, základy programování na grafických kartách a především porozumění molekulárním simulacím, které mají široké uplatnění v řadě dalších oborů (termodynamika, biochemie, materiálové vědy). Téma může být uzpůsobeno preferencím studentky/studenta. 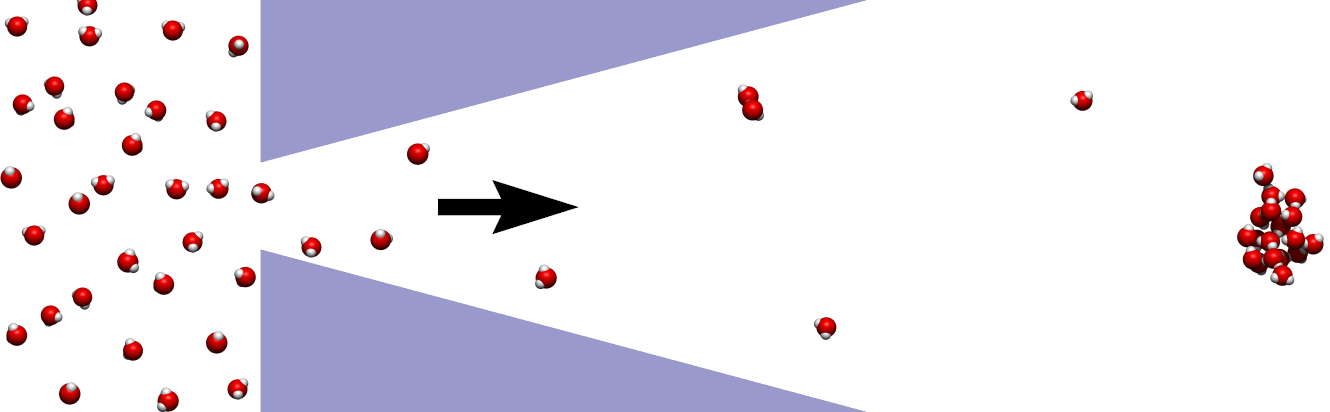 |
| literatura: | [1] Li, C., & Signorell, R. (2021). Understanding vapor nucleation on the molecular level: A review. Journal of Aerosol Science, 153, 105676.
[2] Celný, D., Klíma, M., & Kolafa, J. (2021). Molecular dynamics of heterogeneous systems on GPUs and their application to nucleation in gas expanding to a vacuum. Journal of Chemical Theory and Computation, 17(12), 7397-7405. [3] Celný, David. Development of Parallel Algorithms for Molecular Dynamics Simulation of Heterogeneous Atomistic Systems. Praha, 2023, 176. Disertační práce ČVUT, FJFI; k dispozici v knihovně fakulty. [4] Skupina statistické termodynamiky a molekulových simulací (https://ufch.vscht.cz/veda_a_vyzkum/vyzkumne_skupiny/statisticka_termodynamika) |
| naposledy změněno: | 12.03.2024 21:56:13 |
Matematické modelování šíření lokální koroze u vstřebatelných implantátů
| školitel: | Ing. Karel Tesař, Ph.D. (KMAT FJFI), Ing. Pavel Strachota, Ph.D. (KM FJFI) |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MINF |
| klíčová slova: | vstřebatelné implantáty, lokální koroze, matematické modelování, numerické řešení, simulace |
| přiložený soubor: | |
| popis: | Hlavní příčinou rychlé ztráty mechanických vlastností vstřebatelných zdravotnických prostředků na bázi kovů je koroze, která se objevuje lokálně a následně se šíří. Při statických in vitro testech je pozorována tzv. redepozice korozních produktů, kdy korozní produkty uvolněné z povrchu do okolního média dosedají na nezkorodovaný povrch v okolí, kde vytváří nové galvanické články. V rámci in vitro testování jsou tyto mechanismy poměrně dobře zdokumentovány. Je ovšem otázkou, do jaké míry fungují v živém tělním prostředí (in vivo). Volnému dosedání korozních produktů brání jak dynamické podmínky živého těla a pohyby okolní tkáně, tak přítomnost buněk, vytvářejících mechanickou bariéru a „porézní“ prostředí.
Mechanismy koroze v tělním prostředí je možné zkoumat pomocí matematického modelování, které využívá parciálních diferenciálních rovnic k popisu difuzních a transportních procesů v heterogenním prostředí. V pozdějších fázích vývoje modelu bude třeba implementovat i změny pH a koncentrací iontů v okolí korodujícího hořčíkového implantátu v závislosti na přítomnosti buněčné hmoty. Výsledkem bude úloha, jejíž řešení je nutné hledat numericky pomocí vhodných metod (metoda konečných diferencí, prvků, nebo objemů). K tomuto účelu je možné využít a modifikovat existující softwarové balíky i vývoj vlastního výpočetního kódu. K ověření správnosti výsledků numerických simulací je možno využít výsledků studií prováděných in vitro (ve zkumavce) a in vivo (v živém). Téma je vhodné pro studenty všech stupňů studia. Student se seznámí s medicínským pozadím problému a s technikami matematického modelování a počítačových simulací. Po zvládnutí elementárního popisu difuze a transportu a jednoduchých numerických metod se bude model postupně rozšiřovat, aby se přiblížil realitě. |
| literatura: | [1] D. Höche, C. Blawert, S. V. Lamaka, N. Scharnagl, C. Mendis, M. L. Zheludkevich: The effect of iron re-deposition on the corrosion of impurity-containing magnesium. Phys. Chem. Chem. Phys. 18, 2016, pp. 1279-1291. https://doi.org/10.1039/C5CP05577F
[2] J. Witten, K. Ribbeck: The particle in the spider\'s web: transport through biological hydrogels. Nanoscale 9, 2017, pp. 8080-8095. https://doi.org/10.1039/C6NR09736G [3] S. Ma, B. Zhou, B. Markert: Numerical simulation of the tissue differentiation and corrosion process of biodegradable magnesium implants during bone fracture healing. ZAMM 98 (12), 2018, pp. 2223-2238. https://doi.org/10.1002/zamm.201700314 [4] F. Arends, R. Baumgärtel, O. Lieleg: Ion-Specific Effects Modulate the Diffusive Mobility of Colloids in an Extracellular Matrix Gel. Langmuir 29 (51), 2013, pp. 15965–15973. https://doi.org/10.1021/la404016y |
| naposledy změněno: | 18.06.2024 14:17:57 |
Analýza obrazu: Korelace snímků z mikroskopických technik s 3D daty z µCT tomografie
| školitel: | Ing. Karel Tesař, Ph.D. (KMAT FJFI), Ing. Pavel Strachota, Ph.D. (KM FJFI) |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF, APIN |
| klíčová slova: | mikrotomografie, hledání řezů v 3D datech, strojové učení, registrace obrazu |
| popis: | V rámci rentgenové mikrotomografie je ve vědeckém výzkumu i ve zdravotnictví často nutné s velkou přesností vyhledávat ve 3D datech takový 2D řez, který odpovídá 2D zobrazení dat jinou technikou [1]. Příkladem může být řez histologickým vzorkem nebo snímek z elektronového mikroskopu. Ve vývoji implantátu se to doposud v nemalém množství případů provádí manuálně, kdy operátor tomografu hledá nejvhodnější řez vizuálně. Automatické vyhledání nejvíce odpovídajícího řezu 3D daty bude složitá úloha, která bude vyžadovat porozumění artefaktům a distorzím experimentálních dat z různých technik. Výsledná metoda by ovšem měla značný vědecký i aplikační potenciál.
Cílem práce bude seznámit se s metodami automatizovaného hledání 2D řezů ve 3D datech s využitím konvenčních algoritmů a strojového učení a následně tyto metody implementovat na hledání uživatelem vybraného 2D řezu z tomografických dat v 3D rekonstrukci. Po vytvoření fungujícího postupu na stejné datové sadě budou vytvořeny metody hledající nejpodobnější 2D řez 3D daty se snímky z jiných technik, především pak histologických řezů. Téma je vhodné pro studenty všech stupňů studia. Student se seznámí s medicínským pozadím problému, metodikou rentgenové tomografie a s technikami analýzy obrazu. 
Obr.: Femur potkana po implantaci vstřebatelného Mg drátu pro vyhodnocení kostní novotvorby a) histologický řez, b) nepřesný řez zvolený ručně z µCT 3D dat, c) detail z a) pomocí skenovací elektronové mikroskopie, d) detail: mapa obsahu fosforu z energiově disperzní spektroskopie. |
| literatura: | [1] https://www.sciencedirect.com/science/article/pii/S8756328217303162 |
| naposledy změněno: | 29.07.2024 20:49:25 |
Lokální tloušťka vrstev a útvarů: Měření rozměrů ve 2D a 3D vycházející z ImageJ2
| školitel: | Ing. Karel Tesař, Ph.D. (KMAT FJFI), Ing. Pavel Strachota, Ph.D. (KM FJFI) |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF, APIN |
| klíčová slova: | analýza obrazu, elektronová mikroskopie, ImageJ2, segmentace obrazu, tloušťka vrstvev |
| popis: | Měření tloušťky různých vrstev je typická úloha nejen materiálového a korozního inženýrství, ale i medicíny (např. rozměry trámců v houbovité kostní tkáni). Pro analýzu obrazu již existuje široká škála skriptů v rozšířeném, volně dostupném, programu ImageJ2 [1], využívajícím svůj vlastní skriptovací jazyk ImageJ Macro language (IJM) [2,3]. Přestože tyto prostředky poskytují zajímavé úvodní odhady, je třeba je přizpůsobit konkrétním aplikacím. To lze realizovat jak úpravou volně přístupných skriptů pro ImageJ2, tak přepsáním těchto algoritmů do jiného prostředí, včetně využití strojového učení pro segmentaci a rekonstrukci nedokonalých naměřených dat.
Cílem práce bude se seznámit s dostupnými možnostmi analýzy tloušťky korozních produktů na 2D snímcích z elektronové mikroskopie a s možnostmi segmentace obrazu. Získané poznatky budou aplikovány na korozi Mg-0.4Zn drátů v simulovaném tělním prostředí, kde současně dostupné metody z různých důvodů neposkytují přesné výsledky. Získané distribuce tloušťky korozní vrstvy budou využity pro popis lokalizace koroze, jako jednoho z hlavních faktorů ztráty mechanických vlastností drátů vyrobených z tělem vstřebatelných kovů. Téma je vhodné pro studenty všech stupňů studia. Student se seznámí s medicínským pozadím problému a s technikami analýzy obrazu. Po zvládnutí již implementovaných obecných metod je student bude rozšiřovat o funkcionality zpřesňující jejich výsledky pro konkrétní aplikaci (např. pro různé definice tloušťky vrstvy a pro lokální defekty).  |
| literatura: | [1] https://imagej.net/software/fiji/
[2] https://imagej.net/imagej-wiki-static/Local_Thickness [3] https://github.com/peterjlee/asc-ImageJ-LayerThickness |
| naposledy změněno: | 29.07.2024 20:55:00 |
Spektrální optimalizace pro metrické grafy
| školitel: | Dr. Vladimir Lotoreichik, Ph.D., DSc. |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MINF |
| klíčová slova: | metrický graf, vlastní hodnoty, optimalizace, diferenciální operátor |
| odkaz: | http://aamp.fjfi.cvut.cz/lotoreichik |
| přiložený soubor: | |
| popis: | Téma navrhované závěrečné práce je optimalizace vlastních hodnot diferenciálních operátorů druhého řádu na metrickém grafu
vzhledem k délkám hran a topologické struktuře grafu. Původní fyzikální motivace diferenciálních operátorů
na metrických grafech je popis chování svobodných elektronů v organických molekulách. Podobné modely se používají také pro popis nových materiálů
jako grafen. V současné době spektrální geometrie na metrických grafech je samostatným oborem v matematice.
Co se týče optimalizací na grafech, poměrně dobře prozkoumaný případ
je ten, ve kterém hraniční podmínka ve všech uzlech je Kirchhoffova.
Cílem práce je porozumět docela přirozenému případu, který doposud nebyl dostatečně prozkoumán, ve kterém hraniční podmínka ve vnitřních vrcholech grafu zůstává Kirchhoffova, ale v listech grafu budeme uvažovat jiné hraniční podmínky. Navržené téma vyžaduje určité znalosti z matematické analýzy a obyčejných diferenciálních rovnic. Během analýzy modelu na grafu se student seznámí s metodami, které budou také užitečné pro optimalizace ve vyšších dimenzích, což může být součástí navazující diplomové nebo disertační práce. |
| literatura: | [1] G. Berkolaiko and P. Kuchment, Introduction to quantum graphs, American Mathematical Society, Providence, 2013.
[2] P. Kurasov, Spectral geometry of graphs, Operator Theory: Advances and Applications 293, Birkhauser, Berlin, 2024. |
| naposledy změněno: | 01.08.2024 15:25:04 |
Numerické metody pro parametrické zobecněné rovnice
| školitel: | RNDr. Tomáš Roubal, PhD. |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MINF |
| klíčová slova: | Zobecněné rovnice, Nelineární optimalizace, Josephy-Newton metoda, Semismooth* metoda, Path-following |
| popis: | Hlavní výzvou při řešení nelineárních optimalizačních úloh je efektivní zvládnutí nehladkosti a silné nelinearity, které se často vyskytují v praktických aplikacích. Dvě významné numerické metody, které se touto problematikou zabývají, jsou Josephy-Newton metoda a Semismooth* metoda. Obě metody lze využít k sledování trajektorií řešení (path-following) v různých typech optimalizačních úloh nebo zobecněných rovnicích, které zahrnují operátory s možnou mnohoznačností, tj. operátory, které nemají jednoznačně definované hodnoty pro všechny vstupní parametry. Každá z těchto metod nabízí specifické přístupy k řešení problémů spojených s nehladkostí a nelinearitou.
Josephy-Newton metoda pro path-following využívá koncept zobecněných rovnic, kde se aproximuje pouze jednoznačná část rovnice. Tato metoda je založena na vytváření Newtonových kroků, které umožňují přesné sledování trajektorií řešení za předpokladu dostatečné hladkosti jednoznačné části a regularity operátorů. Semismooth* metoda je obecně navržena pro řešení úloh, kde se vyskytují mnohoznačné operátory. Tato metoda pracuje s konceptem Semismooth* operátorů, což je podmnožina mnohoznačných operátorů, které umožňují aplikaci Newtonovských technik. Mechanismy konvergence a efektivity těchto metod lze zkoumat pomocí numerických simulací, které využívají metody konečných diferencí, konečných prvků nebo konečných objemů k řešení parciálních diferenciálních rovnic popisujících například optimalizační úlohy. Toto téma je vhodné pro studenty vyšších ročníků, kteří se chtějí seznámit s pokročilými technikami numerického modelování a řešení složitých optimalizačních úloh v přítomnosti mnohoznačných operátorů. Cíle práce: 1. Nastudování Josephy-Newton a Semismooth* metod a nástrojů Variační analýzy. 2. Provedení numerických simulací na úlohy v mechanice, elektrických obvodech apod. 3. Zhodnocení a srovnání konvergence a efektivity numerických metod. |
| literatura: | [1] Dontchev, A. L., Krastanov, M. I., Rockafellar, R. T., and Veliov, V. An Euler-Newton continuation method for tracking solution trajectories of parametric variational inequalities. SIAM J. Control Optim. 51, 3 (2013), 1823-1840.
[2] Cibulka, R., and Roubal, T. Solution stability and path-following for a class of generalized equations. In Control systems and mathematical methods in economics, vol. 687 of Lecture Notes in Econom. and Math. Systems. Springer, Cham, 2018, pp. 57-80. [3] Gfrerer, H., and Outrata, J. On a semismooth* Newton method for solving generalized equations. SIAM J. Optim. 31, 1 (2021), 489-517. |
| naposledy změněno: | 04.09.2024 22:46:55 |
Zpracování výsledků masivní nanoindentace
| školitel: | Prof. Dr. Ing. Petr Haušild, doc. Ing. Aleš Materna, Ph.D. |
| e-mail: | zobrazit e-mail |
| typ práce: | bakalářská práce, diplomová práce |
| zaměření: | MI_MM, MI_AMSM, MINF |
| klíčová slova: | statistické rozdělení, nanoindentace, vícefázové materiály |
| přiložený soubor: | |
| popis: | Cílem navrhovaného tématu je vyvinutí metodiky měření materiálových charakteristik strukturních fází u materiálů s heterogenní strukturou (tj. v případech, kdy strukturní fáze mají odlišné hodnoty tvrdosti a/nebo Youngova modulu). Je třeba si uvědomit, že výsledky měření tvrdosti pomocí nanoindentace ve vícefázových materiálech mohou být významně ovlivněny přítomností rozhraní mezi sousedními materiály. V některých případech totiž nelze zcela zamezit indentaci v blízkosti rozhraní. Při maticové indentaci s velkým počtem vtisků může poloha některých vtisků koincidovat s fázovým rozhraním na povrchu, případně s rozhraním skrytým pod povrchem vzorku. Výsledné hodnoty tak mohou být významně ovlivněny, aniž bychom to byli schopni odhalit např. použitím korelativní mikroskopie. Navrhovaná metodika by měla zahrnout vliv hloubky vtisku a charakteristické délky mikrostruktury na měřený modul, respektive na hodnoty tvrdosti a podmíněnou pravděpodobnost indentace v blízkosti (i skrytého) rozhraní. V rámci bakalářské/diplomové práce by měl být vyvinut a implementován algoritmus umožňující efektivní identifikaci parametrů statistického rozdělení materiálových charakteristik, ale v případě zájmu je možné i zapojení studenta do experimentální práce v laboratoři mikro/nanoindentace nebo dalšího zpracování naměřených dat například s využitím umělé inteligence. Detaily tématu rád odpovím osobně (KMAT 3. patro Trojanova) nebo emailem.
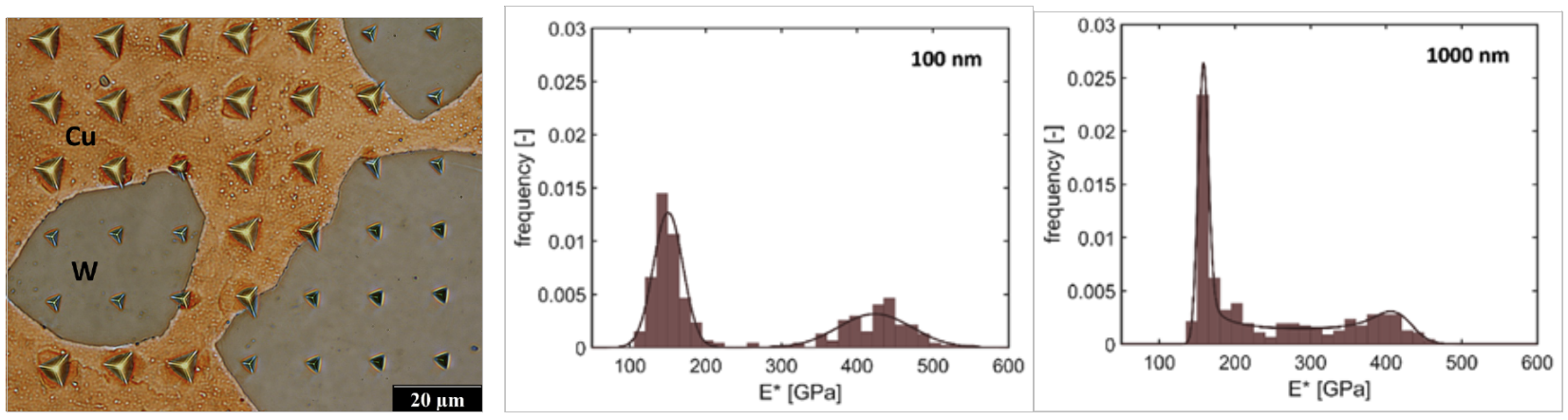
Obr.: Maticová indentace ve dvoufázovém materiálu (W-Cu). Snímek vlevo ilustruje vliv rozhraní mezi odlišnými fázemi na velikost měřených vtisků, histogramy vpravo pak změnu rozdělení naměřených hodnot určených při indentaci ve stejných místech, ale při různých hloubkách vtisků. |
| literatura: | Haušild, P., Materna, A., Kocmanová, L., Matějíček J. https://doi.org/10.1557/jmr.2016.37
Haušild, P., Čech, J., Materna, A., Matějíček J. https://doi.org/10.1016/j.mechmat.2018.11.006 Randall, N.X., Vandamme, M. & Ulm, FJ. https://doi.org/10.1557/jmr.2009.0149 |
| naposledy změněno: | 02.04.2025 10:35:18 |
Databáze V3S
Aplikace V3S eviduje výsledky vědy a výzkumu a další aktivity vědecko-výzkumných pracovníků ve vědecké komunitě. Aplikace V3S slouží k odesílání výsledků do RIV, exportům pro statistické analýzy i k interním hodnocením vědecko-výzkumné činnosti.
Seznam publikaci ve V3S
Články v časopisech
2018
Michal Beneš and Radek Fučík and Vladimír Havlena
and Vladimír Klement and Miroslav Kolář and Ondřej
Polívka and Jakub Solovský and Pavel Strachota, An Efficient and Robust Numerical Solution of the Full-Order Multiscale
Model of Lithium-Ion Battery, Math. Probl. Eng. 2018 (2018) , 12pages
BiBTeX
BiBTeX
@ARTICLE{Math_Prob_En,
title = {An Efficient and Robust Numerical Solution of the Full-Order Multiscale Model of Lithium-Ion Battery},
author = {Michal Beneš and Radek Fučík and Vladimír Havlena and Vladimír Klement and Miroslav Kolář and Ondřej Polívka and Jakub Solovský and Pavel Strachota},
journal = {Math. Probl. Eng.},
year = {2018},
volume = {2018},
pages = {12pages}
}
title = {An Efficient and Robust Numerical Solution of the Full-Order Multiscale Model of Lithium-Ion Battery},
author = {Michal Beneš and Radek Fučík and Vladimír Havlena and Vladimír Klement and Miroslav Kolář and Ondřej Polívka and Jakub Solovský and Pavel Strachota},
journal = {Math. Probl. Eng.},
year = {2018},
volume = {2018},
pages = {12pages}
}
2017
Pavel Strachota and Michal Beneš, Error estimate of the finite volume scheme for the Allen-Cahn equation, BIT 2017 (2017) , 1-19
BiBTeX
BiBTeX
@ARTICLE{BIT-Error_es,
title = {Error estimate of the finite volume scheme for the Allen-Cahn equation},
author = {Pavel Strachota and Michal Beneš},
journal = {BIT},
year = {2017},
volume = {2017},
pages = {1--19}
}
title = {Error estimate of the finite volume scheme for the Allen-Cahn equation},
author = {Pavel Strachota and Michal Beneš},
journal = {BIT},
year = {2017},
volume = {2017},
pages = {1--19}
}
Jan Mach and Michal Beneš and Pavel Strachota, Nonlinear Galerkin Finite Element Method Applied to the System of
Reaction-Diffusion Equations in One Space Dimension, Comput. Math. Appl. 73 (2017) , 2053-2065
BiBTeX
BiBTeX
@ARTICLE{NLG-Honza-20,
title = {Nonlinear Galerkin Finite Element Method Applied to the System of Reaction-Diffusion Equations in One Space Dimension},
author = {Jan Mach and Michal Beneš and Pavel Strachota},
journal = {Comput. Math. Appl.},
year = {2017},
volume = {73},
number = {9},
pages = {2053--2065}
}
title = {Nonlinear Galerkin Finite Element Method Applied to the System of Reaction-Diffusion Equations in One Space Dimension},
author = {Jan Mach and Michal Beneš and Pavel Strachota},
journal = {Comput. Math. Appl.},
year = {2017},
volume = {73},
number = {9},
pages = {2053--2065}
}
2015
Petr Bauer and Michal Beneš and Radek Fučík and Hung
Dieu Hoang and Vladimír Klement and Radek Máca and Jan Mach
and Tomáš Oberhuber and Pavel Strachota and Vítězslav
Žabka and Vladimír Havlena, Numerical Simulation of Flow in Fluidized Beds, Discrete. Cont. Dyn. S. S 8 (2015) , 833-846
BiBTeX
BiBTeX
@ARTICLE{Honeywell-CJ,
title = {Numerical Simulation of Flow in Fluidized Beds},
author = {Petr Bauer and Michal Beneš and Radek Fučík and Hung Dieu Hoang and Vladimír Klement and Radek Máca and Jan Mach and Tomáš Oberhuber and Pavel Strachota and Vítězslav Žabka and Vladimír Havlena},
journal = {Discrete. Cont. Dyn. S. S},
year = {2015},
volume = {8},
number = {5},
pages = {833-846}
}
title = {Numerical Simulation of Flow in Fluidized Beds},
author = {Petr Bauer and Michal Beneš and Radek Fučík and Hung Dieu Hoang and Vladimír Klement and Radek Máca and Jan Mach and Tomáš Oberhuber and Pavel Strachota and Vítězslav Žabka and Vladimír Havlena},
journal = {Discrete. Cont. Dyn. S. S},
year = {2015},
volume = {8},
number = {5},
pages = {833-846}
}
2012
Pavel Strachota and Michal Beneš and Jaroslav Tintěra, Towards Clinical Applicability of the Diffusion-based DT-MRI Visualization
Algorithm, J. Vis. Commun. Image R. 23 (2012) , 387-396
BiBTeX
BiBTeX
@ARTICLE{JVCIR2012,
title = {Towards Clinical Applicability of the Diffusion-based {DT-MRI} Visualization Algorithm},
author = {Pavel Strachota and Michal Beneš and Jaroslav Tintěra},
journal = {J. Vis. Commun. Image R.},
year = {2012},
volume = {23},
number = {2},
pages = {387--396}
}
title = {Towards Clinical Applicability of the Diffusion-based {DT-MRI} Visualization Algorithm},
author = {Pavel Strachota and Michal Beneš and Jaroslav Tintěra},
journal = {J. Vis. Commun. Image R.},
year = {2012},
volume = {23},
number = {2},
pages = {387--396}
}
Michal Beneš and Tomáš Oberhuber and Pavel Strachota
and Robert Straka and Vladimír Havlena, Mathematical modelling of combustion and biofuel co-firing in industrial
steam generators, RIMS Kokyuroku B35 (2012) , 141-157
BiBTeX
BiBTeX
@ARTICLE{RIMS2011,
title = {Mathematical modelling of combustion and biofuel co-firing in industrial steam generators},
author = {Michal Beneš and Tomáš Oberhuber and Pavel Strachota and Robert Straka and Vladimír Havlena},
journal = {RIMS Kokyuroku},
year = {2012},
volume = {B35},
pages = {141--157}
}
title = {Mathematical modelling of combustion and biofuel co-firing in industrial steam generators},
author = {Michal Beneš and Tomáš Oberhuber and Pavel Strachota and Robert Straka and Vladimír Havlena},
journal = {RIMS Kokyuroku},
year = {2012},
volume = {B35},
pages = {141--157}
}
2009
Pavel Strachota, Implementation of the \uppercaseMR Tractography Visualization Kit
Based on the Anisotropic Allen-Cahn Equation, Kybernetika 45 (2009) , 657-669
BiBTeX
BiBTeX
@ARTICLE{CJS2008-Kybe,
title = {Implementation of the \uppercase{MR} Tractography Visualization Kit Based on the Anisotropic {A}llen-{C}ahn Equation},
author = {Pavel Strachota},
journal = {Kybernetika},
year = {2009},
volume = {45},
number = {4},
pages = {657--669}
}
title = {Implementation of the \uppercase{MR} Tractography Visualization Kit Based on the Anisotropic {A}llen-{C}ahn Equation},
author = {Pavel Strachota},
journal = {Kybernetika},
year = {2009},
volume = {45},
number = {4},
pages = {657--669}
}
Články ve sbornících
2016
Pavel Strachota and Michal Beneš, A Hybrid Parallel Numerical Algorithm for Three-Dimensional Phase
Field Modeling of Crystal Growth, ALGORITMY 2016, 20th Conference on Scientific Computing, Vysok?
Tatry - Podbanské, Slovakia, March 14 - 18, 2016. Proceedings
of contributed papers and posters, (2016) , 23-32, Comenius University, Bratislava
BiBTeX
BiBTeX
@INPROCEEDINGS{ALGORITMY201,
title = {A Hybrid Parallel Numerical Algorithm for Three-Dimensional Phase Field Modeling of Crystal Growth},
author = {Pavel Strachota and Michal Beneš},
booktitle = {ALGORITMY 2016, 20th Conference on Scientific Computing, Vysok? Tatry - Podbanské, Slovakia, March 14 - 18, 2016. Proceedings of contributed papers and posters},
editor = {Angela Handlovičová and Daniel ševčovič},
publisher = {Comenius University, Bratislava},
year = {2016},
pages = {23--32}
}
title = {A Hybrid Parallel Numerical Algorithm for Three-Dimensional Phase Field Modeling of Crystal Growth},
author = {Pavel Strachota and Michal Beneš},
booktitle = {ALGORITMY 2016, 20th Conference on Scientific Computing, Vysok? Tatry - Podbanské, Slovakia, March 14 - 18, 2016. Proceedings of contributed papers and posters},
editor = {Angela Handlovičová and Daniel ševčovič},
publisher = {Comenius University, Bratislava},
year = {2016},
pages = {23--32}
}
2014
Michal Beneš and Pavel Strachota and Radek Máca and Vladimír
Havlena and Jan Mach, A Quasi-1D Model of Biomass Co-Firing in a Circulating Fluidized
Bed Boiler, Finite Volumes for Complex Applications VII - Elliptic, Parabolic,
and Hyperbolic Problems, (2014) , 791-799, Springer
BiBTeX
BiBTeX
@INPROCEEDINGS{FVCA7-2014,
title = {A Quasi-{1D} Model of Biomass Co-Firing in a Circulating Fluidized Bed Boiler},
author = {Michal Beneš and Pavel Strachota and Radek Máca and Vladimír Havlena and Jan Mach},
booktitle = {Finite Volumes for Complex Applications VII - Elliptic, Parabolic, and Hyperbolic Problems},
editor = {J\"{u}rgen Fuhrmann and Mario Ohlberger and Christian Rohde},
publisher = {Springer},
year = {2014},
volume = {78},
series = {Springer Proceedings in Mathematics \& Statistics},
pages = {791--799}
}
title = {A Quasi-{1D} Model of Biomass Co-Firing in a Circulating Fluidized Bed Boiler},
author = {Michal Beneš and Pavel Strachota and Radek Máca and Vladimír Havlena and Jan Mach},
booktitle = {Finite Volumes for Complex Applications VII - Elliptic, Parabolic, and Hyperbolic Problems},
editor = {J\"{u}rgen Fuhrmann and Mario Ohlberger and Christian Rohde},
publisher = {Springer},
year = {2014},
volume = {78},
series = {Springer Proceedings in Mathematics \& Statistics},
pages = {791--799}
}
2013
Pavel Strachota and Michal Beneš, Design and Verification of the MPFA Scheme for Three-Dimensional
Phase Field Model of Dendritic Crystal Growth, Numerical Mathematics and Advanced Applications 2011: Proceedings
of ENUMATH 2011, the 9th European Conference on Numerical Mathematics
and Advanced Applications, Leicester, September 2011, (2013) , 459-467, Springer Berlin Heidelberg
BiBTeX
BiBTeX
@INPROCEEDINGS{ENUMATH2011,
title = {Design and Verification of the {MPFA} Scheme for Three-Dimensional Phase Field Model of Dendritic Crystal Growth},
author = {Pavel Strachota and Michal Beneš},
booktitle = {Numerical Mathematics and Advanced Applications 2011: Proceedings of {ENUMATH} 2011, the 9th European Conference on Numerical Mathematics and Advanced Applications, Leicester, September 2011},
editor = {Andrea Cangiani and Ruslan L. Davidchack and Emmanuil Georgoulis and Alexander N. Gorban and Jeremy Levesley and Michael V. Tretyakov},
publisher = {Springer Berlin Heidelberg},
year = {2013},
pages = {459--467}
}
title = {Design and Verification of the {MPFA} Scheme for Three-Dimensional Phase Field Model of Dendritic Crystal Growth},
author = {Pavel Strachota and Michal Beneš},
booktitle = {Numerical Mathematics and Advanced Applications 2011: Proceedings of {ENUMATH} 2011, the 9th European Conference on Numerical Mathematics and Advanced Applications, Leicester, September 2011},
editor = {Andrea Cangiani and Ruslan L. Davidchack and Emmanuil Georgoulis and Alexander N. Gorban and Jeremy Levesley and Michael V. Tretyakov},
publisher = {Springer Berlin Heidelberg},
year = {2013},
pages = {459--467}
}
2012
Petr Bauer and Vladimír Klement and Pavel Strachota and Vít
Žabka, Numerical Study of Flow in a 2D Boiler, ALGORITMY 2012 - Proceedings of Contributed Papers and Posters, (2012) , 172-178, Slovak University of Technology in Bratislava
BiBTeX
BiBTeX
@INPROCEEDINGS{ALGORITMY201,
title = {Numerical Study of Flow in a 2D Boiler},
author = {Petr Bauer and Vladimír Klement and Pavel Strachota and Vít Žabka},
booktitle = {ALGORITMY 2012 - Proceedings of Contributed Papers and Posters},
editor = {Angela Handlovičová and Zuzana Minarechová and Daniel ševčovič},
publisher = {Slovak University of Technology in Bratislava},
year = {2012},
pages = {172--178}
}
title = {Numerical Study of Flow in a 2D Boiler},
author = {Petr Bauer and Vladimír Klement and Pavel Strachota and Vít Žabka},
booktitle = {ALGORITMY 2012 - Proceedings of Contributed Papers and Posters},
editor = {Angela Handlovičová and Zuzana Minarechová and Daniel ševčovič},
publisher = {Slovak University of Technology in Bratislava},
year = {2012},
pages = {172--178}
}
2011
Pavel Strachota and Michal Beneš, A Multipoint Flux Approximation Finite Volume Scheme for Solving
Anisotropic Reaction-Diffusion Systems in \uppercase3D, Finite Volumes for Complex Applications VI - Problems & Perspectives, (2011) , 741-749, Springer
BiBTeX
BiBTeX
@INPROCEEDINGS{FVCA6-2011,
title = {A Multipoint Flux Approximation Finite Volume Scheme for Solving Anisotropic Reaction-Diffusion Systems in \uppercase{3D}},
author = {Pavel Strachota and Michal Beneš},
booktitle = {Finite Volumes for Complex Applications VI - Problems \& Perspectives},
editor = {Jaroslav Fořt and Jiří F\"{u}rst and Jan Halama and Rapha\`{e}le Herbin and Florence Hubert},
publisher = {Springer},
year = {2011},
pages = {741--749}
}
title = {A Multipoint Flux Approximation Finite Volume Scheme for Solving Anisotropic Reaction-Diffusion Systems in \uppercase{3D}},
author = {Pavel Strachota and Michal Beneš},
booktitle = {Finite Volumes for Complex Applications VI - Problems \& Perspectives},
editor = {Jaroslav Fořt and Jiří F\"{u}rst and Jan Halama and Rapha\`{e}le Herbin and Florence Hubert},
publisher = {Springer},
year = {2011},
pages = {741--749}
}
2010
Pavel Strachota and Michal Beneš and Marco Grottadaurea and Jaroslav
Tintěra, Analysis of the Parallel Finite Volume Solver for the Anisotropic
Allen-Cahn Equation in 3D, Numerical Mathematics and Advanced Applications 2009: Proceedings
of ENUMATH 2009, the 8th European Conference on Numerical Mathematics
and Advanced Applications, Uppsala, July 2009, (2010) , 839-846, Springer Berlin Heidelberg
BiBTeX
BiBTeX
@INPROCEEDINGS{ENUMATH2009,
title = {Analysis of the Parallel Finite Volume Solver for the Anisotropic {A}llen-{C}ahn Equation in {3D}},
author = {Pavel Strachota and Michal Beneš and Marco Grottadaurea and Jaroslav Tintěra},
booktitle = {Numerical Mathematics and Advanced Applications 2009: Proceedings of {ENUMATH} 2009, the 8th European Conference on Numerical Mathematics and Advanced Applications, Uppsala, July 2009},
editor = {Gunilla Kreiss and Per L\"{o}tstedt and Axel M{\aa}lqvist and Maya Neytcheva},
publisher = {Springer Berlin Heidelberg},
year = {2010},
pages = {839--846}
}
title = {Analysis of the Parallel Finite Volume Solver for the Anisotropic {A}llen-{C}ahn Equation in {3D}},
author = {Pavel Strachota and Michal Beneš and Marco Grottadaurea and Jaroslav Tintěra},
booktitle = {Numerical Mathematics and Advanced Applications 2009: Proceedings of {ENUMATH} 2009, the 8th European Conference on Numerical Mathematics and Advanced Applications, Uppsala, July 2009},
editor = {Gunilla Kreiss and Per L\"{o}tstedt and Axel M{\aa}lqvist and Maya Neytcheva},
publisher = {Springer Berlin Heidelberg},
year = {2010},
pages = {839--846}
}
2009
Pavel Strachota, Antidissipative Numerical Schemes for the Anisotropic Diffusion Operator
in Problems for the Allen-Cahn Equation, ALGORITMY 2009 - Proceedings of contributed lectures and posters, (2009) , 134-142, Slovak University of Technology in Bratislava
BiBTeX
BiBTeX
@INPROCEEDINGS{ALGORITMY200,
title = {Antidissipative Numerical Schemes for the Anisotropic Diffusion Operator in Problems for the {A}llen-{C}ahn Equation},
author = {Pavel Strachota},
booktitle = {ALGORITMY 2009 - Proceedings of contributed lectures and posters},
editor = {Angela Handlovičová and Peter Frolkovič and Karol Mikula and Daniel ševčovič},
publisher = {Slovak University of Technology in Bratislava},
year = {2009},
volume = {18},
pages = {134--142}
}
title = {Antidissipative Numerical Schemes for the Anisotropic Diffusion Operator in Problems for the {A}llen-{C}ahn Equation},
author = {Pavel Strachota},
booktitle = {ALGORITMY 2009 - Proceedings of contributed lectures and posters},
editor = {Angela Handlovičová and Peter Frolkovič and Karol Mikula and Daniel ševčovič},
publisher = {Slovak University of Technology in Bratislava},
year = {2009},
volume = {18},
pages = {134--142}
}
Pavel Strachota, Application of Anisotropic Diffusion in \uppercaseMR Tractography, Science and Supercomputing in Europe - Report 2008, (2009) , 279-284, CINECA Consorzio Interuniversitario
BiBTeX
BiBTeX
@INPROCEEDINGS{CINECA2008,
title = {Application of Anisotropic Diffusion in \uppercase{MR} Tractography},
author = {Pavel Strachota},
address = {Bologna},
booktitle = {Science and Supercomputing in Europe - Report 2008},
publisher = {CINECA Consorzio Interuniversitario},
year = {2009},
pages = {279--284}
}
title = {Application of Anisotropic Diffusion in \uppercase{MR} Tractography},
author = {Pavel Strachota},
address = {Bologna},
booktitle = {Science and Supercomputing in Europe - Report 2008},
publisher = {CINECA Consorzio Interuniversitario},
year = {2009},
pages = {279--284}
}
2008
Pavel Strachota, Anisotropic Diffusion In Mathematical Visualization, Science and Supercomputing in Europe - Report 2007, (2008) , 826-831, CINECA Consorzio Interuniversitario
BiBTeX
BiBTeX
@INPROCEEDINGS{CINECA2007,
title = {Anisotropic Diffusion In Mathematical Visualization},
author = {Pavel Strachota},
address = {Bologna},
booktitle = {Science and Supercomputing in Europe - Report 2007},
publisher = {CINECA Consorzio Interuniversitario},
year = {2008},
pages = {826--831}
}
title = {Anisotropic Diffusion In Mathematical Visualization},
author = {Pavel Strachota},
address = {Bologna},
booktitle = {Science and Supercomputing in Europe - Report 2007},
publisher = {CINECA Consorzio Interuniversitario},
year = {2008},
pages = {826--831}
}
Michal Beneš and Pavel Strachota and Zdeněk čulík, Quantitative Aspects of Microstructure Formation in Solidification, Multiscale Materials Modeling 2008, (2008) , 746-751, Florida State University
BiBTeX
BiBTeX
@INPROCEEDINGS{MMM2008,
title = {Quantitative Aspects of Microstructure Formation in Solidification},
author = {Michal Beneš and Pavel Strachota and Zdeněk čulík},
booktitle = {Multiscale Materials Modeling 2008},
editor = {El-Azab},
publisher = {Florida State University},
year = {2008},
pages = {746--751}
}
title = {Quantitative Aspects of Microstructure Formation in Solidification},
author = {Michal Beneš and Pavel Strachota and Zdeněk čulík},
booktitle = {Multiscale Materials Modeling 2008},
editor = {El-Azab},
publisher = {Florida State University},
year = {2008},
pages = {746--751}
}
Pavel Strachota, Vector Field Visualization by means of Anisotropic Diffusion, , () , 193-205,
BiBTeX
BiBTeX
@INPROCEEDINGS{CJS2006-pave,
title = {Vector Field Visualization by means of Anisotropic Diffusion},
author = {Pavel Strachota},
pages = {193--205}
}
title = {Vector Field Visualization by means of Anisotropic Diffusion},
author = {Pavel Strachota},
pages = {193--205}
}
Pavel Strachota and Michal Beneš and Marco Grottadaurea, Computational Investigation and Assessment of Numerical Schemes for
Anisotropic Diffusion Equations, , () , 73-83,
BiBTeX
BiBTeX
@INPROCEEDINGS{CJS2010-pave,
title = {Computational Investigation and Assessment of Numerical Schemes for Anisotropic Diffusion Equations},
author = {Pavel Strachota and Michal Beneš and Marco Grottadaurea},
pages = {73--83}
}
title = {Computational Investigation and Assessment of Numerical Schemes for Anisotropic Diffusion Equations},
author = {Pavel Strachota and Michal Beneš and Marco Grottadaurea},
pages = {73--83}
}
Ostatní publikace
2015
Michal Beneš and Pavel Strachota and Dejan Kirda and Alexandr
Žák, Xhaust: Infinity Phase Flow Simulation in Automobile Exhaust Pipe
- Instructions for Use of the Xhaust Software Package Version 2.0
(Xhaust-NU IPF, Milestone II release), 2015
BiBTeX
BiBTeX
@TECHREPORT{BOSCH-Milest,
title = {Xhaust: Infinity Phase Flow Simulation in Automobile Exhaust Pipe - Instructions for Use of the {X}haust Software Package Version 2.0 ({X}haust-{NU IPF}, Milestone {II} release)},
author = {Michal Beneš and Pavel Strachota and Dejan Kirda and Alexandr Žák},
institution = {Czech Technical University in Prague},
year = {2015}
}
title = {Xhaust: Infinity Phase Flow Simulation in Automobile Exhaust Pipe - Instructions for Use of the {X}haust Software Package Version 2.0 ({X}haust-{NU IPF}, Milestone {II} release)},
author = {Michal Beneš and Pavel Strachota and Dejan Kirda and Alexandr Žák},
institution = {Czech Technical University in Prague},
year = {2015}
}
Michal Beneš and Pavel Strachota and Dejan Kirda and Alexandr
Žák, Xhaust: Progress in the Development of the Quasi-1D CFD Model
of Automobile Exhaust Pipe Flow with Condensation, 2015
BiBTeX
BiBTeX
@TECHREPORT{BOSCH-Milest,
title = {Xhaust: Progress in the Development of the Quasi-{1D} {CFD} Model of Automobile Exhaust Pipe Flow with Condensation},
author = {Michal Beneš and Pavel Strachota and Dejan Kirda and Alexandr Žák},
institution = {Czech Technical University in Prague},
year = {2015}
}
title = {Xhaust: Progress in the Development of the Quasi-{1D} {CFD} Model of Automobile Exhaust Pipe Flow with Condensation},
author = {Michal Beneš and Pavel Strachota and Dejan Kirda and Alexandr Žák},
institution = {Czech Technical University in Prague},
year = {2015}
}
Michal Beneš and Pavel Strachota and Dejan Kirda and Alexandr
Žák, Xhaust: Infinity Phase Flow Simulation in Automobile Exhaust Pipe, 2015
BiBTeX
BiBTeX
@TECHREPORT{BOSCH-Milest,
title = {Xhaust: Infinity Phase Flow Simulation in Automobile Exhaust Pipe},
author = {Michal Beneš and Pavel Strachota and Dejan Kirda and Alexandr Žák},
institution = {Czech Technical University in Prague},
year = {2015}
}
title = {Xhaust: Infinity Phase Flow Simulation in Automobile Exhaust Pipe},
author = {Michal Beneš and Pavel Strachota and Dejan Kirda and Alexandr Žák},
institution = {Czech Technical University in Prague},
year = {2015}
}
Michal Beneš and Radek Fučík and Vladimír Havlena
and Dejan Kirda and Vladimír Klement and Miroslav Kolář
and Ondřej Polívka and Pavel Strachota, Development of Numerical Model of Lithium-Ion Cell Dynamics and Energy
Exchange, 2015
BiBTeX
BiBTeX
@TECHREPORT{Honeywell-20,
title = {Development of Numerical Model of Lithium-Ion Cell Dynamics and Energy Exchange},
author = {Michal Beneš and Radek Fučík and Vladimír Havlena and Dejan Kirda and Vladimír Klement and Miroslav Kolář and Ondřej Polívka and Pavel Strachota},
institution = {Czech Technical University in Prague},
year = {2015}
}
title = {Development of Numerical Model of Lithium-Ion Cell Dynamics and Energy Exchange},
author = {Michal Beneš and Radek Fučík and Vladimír Havlena and Dejan Kirda and Vladimír Klement and Miroslav Kolář and Ondřej Polívka and Pavel Strachota},
institution = {Czech Technical University in Prague},
year = {2015}
}
2014
Michal Beneš and Pavel Strachota and Jan Mach, A Quasi-1D Two-Phase Model for Exhaust Pipe Flow with Condensation, 2014
BiBTeX
BiBTeX
@TECHREPORT{BOSCH-Milest,
title = {A Quasi-{1D} Two-Phase Model for Exhaust Pipe Flow with Condensation},
author = {Michal Beneš and Pavel Strachota and Jan Mach},
institution = {Czech Technical University in Prague},
year = {2014}
}
title = {A Quasi-{1D} Two-Phase Model for Exhaust Pipe Flow with Condensation},
author = {Michal Beneš and Pavel Strachota and Jan Mach},
institution = {Czech Technical University in Prague},
year = {2014}
}
Michal Beneš and Pavel Strachota and Vítězslav Žabka
and Tomáš Oberhuber, A Quasi-1D Two-Phase Model for Exhaust Pipe Flow with Condensation
- Instructions for Use of the Xhaust Software Package Version 0.5
(Milestone I), 2014
BiBTeX
BiBTeX
@TECHREPORT{BOSCH-Milest,
title = {A Quasi-{1D} Two-Phase Model for Exhaust Pipe Flow with Condensation - Instructions for Use of the {X}haust Software Package Version 0.5 (Milestone I)},
author = {Michal Beneš and Pavel Strachota and Vítězslav Žabka and Tomáš Oberhuber},
institution = {Czech Technical University in Prague},
year = {2014}
}
title = {A Quasi-{1D} Two-Phase Model for Exhaust Pipe Flow with Condensation - Instructions for Use of the {X}haust Software Package Version 0.5 (Milestone I)},
author = {Michal Beneš and Pavel Strachota and Vítězslav Žabka and Tomáš Oberhuber},
institution = {Czech Technical University in Prague},
year = {2014}
}
Michal Beneš and Pavel Strachota and Vítězslav Žabka
and Tomáš Oberhuber, Design and Computational Implementation of A Quasi-1D Two-Phase
Fluid Dynamics Model for Exhaust Pipe Flow with Condensation, 2014
BiBTeX
BiBTeX
@TECHREPORT{BOSCH-Milest,
title = {Design and Computational Implementation of A Quasi-{1D} Two-Phase Fluid Dynamics Model for Exhaust Pipe Flow with Condensation},
author = {Michal Beneš and Pavel Strachota and Vítězslav Žabka and Tomáš Oberhuber},
institution = {Czech Technical University in Prague},
year = {2014}
}
title = {Design and Computational Implementation of A Quasi-{1D} Two-Phase Fluid Dynamics Model for Exhaust Pipe Flow with Condensation},
author = {Michal Beneš and Pavel Strachota and Vítězslav Žabka and Tomáš Oberhuber},
institution = {Czech Technical University in Prague},
year = {2014}
}
Michal Beneš and Radek Fučík and Vladimír Havlena
and Vladimír Klement and Miroslav Kolář and Ondřej
Polívka and Pavel Strachota and Jiří Vejrosta, Modeling and Simulation of Lithium-Ion Battery Dynamics - Review, 2014
BiBTeX
BiBTeX
@TECHREPORT{Honeywell-20,
title = {Modeling and Simulation of Lithium-Ion Battery Dynamics - Review},
author = {Michal Beneš and Radek Fučík and Vladimír Havlena and Vladimír Klement and Miroslav Kolář and Ondřej Polívka and Pavel Strachota and Jiří Vejrosta},
institution = {Czech Technical University in Prague},
year = {2014}
}
title = {Modeling and Simulation of Lithium-Ion Battery Dynamics - Review},
author = {Michal Beneš and Radek Fučík and Vladimír Havlena and Vladimír Klement and Miroslav Kolář and Ondřej Polívka and Pavel Strachota and Jiří Vejrosta},
institution = {Czech Technical University in Prague},
year = {2014}
}
2013
Michal Beneš and Pavel Strachota and Radek Máca and Vladimír
Havlena and Jan Mach, A Quasi-1D Model of Biomass Co-Firing in a Circulating Fluidized
Bed Boiler, 2013
BiBTeX
BiBTeX
@TECHREPORT{Honeywell-20,
title = {A Quasi-{1D} Model of Biomass Co-Firing in a Circulating Fluidized Bed Boiler},
author = {Michal Beneš and Pavel Strachota and Radek Máca and Vladimír Havlena and Jan Mach},
institution = {Czech Technical University in Prague},
year = {2013}
}
title = {A Quasi-{1D} Model of Biomass Co-Firing in a Circulating Fluidized Bed Boiler},
author = {Michal Beneš and Pavel Strachota and Radek Máca and Vladimír Havlena and Jan Mach},
institution = {Czech Technical University in Prague},
year = {2013}
}
Michal Beneš and Pavel Strachota and Jan Mach and Hung Dieu Hoang
and Vladimír Havlena, Coal and Biomass Particle Burnout Models for use in Pulverized Coal
and Fluidized Bed Combustion Simulations, 2013
BiBTeX
BiBTeX
@TECHREPORT{Honeywell-20,
title = {Coal and Biomass Particle Burnout Models for use in Pulverized Coal and Fluidized Bed Combustion Simulations},
author = {Michal Beneš and Pavel Strachota and Jan Mach and Hung Dieu Hoang and Vladimír Havlena},
institution = {Czech Technical University in Prague},
year = {2013}
}
title = {Coal and Biomass Particle Burnout Models for use in Pulverized Coal and Fluidized Bed Combustion Simulations},
author = {Michal Beneš and Pavel Strachota and Jan Mach and Hung Dieu Hoang and Vladimír Havlena},
institution = {Czech Technical University in Prague},
year = {2013}
}
Michal Beneš and Pavel Strachota and Jan Mach and Hung Dieu Hoang
and Vladimír Havlena and Tomáš Oberhuber and Radek Fučík
and Petr Bauer and Vítězslav Žabka and Vladimír Klement
and Radek Máca, Simulation of Biomass Co-Firing and Pollutant Development in an Industrial
Pulverized Coal Boiler with Air Staging Control, 2013
BiBTeX
BiBTeX
@TECHREPORT{Honeywell-20,
title = {Simulation of Biomass Co-Firing and Pollutant Development in an Industrial Pulverized Coal Boiler with Air Staging Control},
author = {Michal Beneš and Pavel Strachota and Jan Mach and Hung Dieu Hoang and Vladimír Havlena and Tomáš Oberhuber and Radek Fučík and Petr Bauer and Vítězslav Žabka and Vladimír Klement and Radek Máca},
institution = {Czech Technical University in Prague},
year = {2013}
}
title = {Simulation of Biomass Co-Firing and Pollutant Development in an Industrial Pulverized Coal Boiler with Air Staging Control},
author = {Michal Beneš and Pavel Strachota and Jan Mach and Hung Dieu Hoang and Vladimír Havlena and Tomáš Oberhuber and Radek Fučík and Petr Bauer and Vítězslav Žabka and Vladimír Klement and Radek Máca},
institution = {Czech Technical University in Prague},
year = {2013}
}
2012
Pavel Strachota, Analysis and Application of Numerical Methods for Solving Nonlinear
Reaction-Diffusion Equations, Czech Technical University in Prague, 2012
BiBTeX
BiBTeX
@PHDTHESIS{dissertation,
title = {Analysis and Application of Numerical Methods for Solving Nonlinear Reaction-Diffusion Equations},
author = {Pavel Strachota},
year = {2012},
school = {Czech Technical University in Prague}
}
title = {Analysis and Application of Numerical Methods for Solving Nonlinear Reaction-Diffusion Equations},
author = {Pavel Strachota},
year = {2012},
school = {Czech Technical University in Prague}
}
za obsah této stránky zodpovídá:
Radek Fučík | naposledy změněno: 7.8.2011